各相関係数に関する問題です。
相関係数と名のつく概念は多くあるので、それらの弁別を前提とした問題は出やすいところでしょうね。
問83 相関関係を求める2つの変数それぞれから、共通の第3の変数の影響を除いて求められる相関係数として、最も適切なものを1つ選べ。
① 重相関係数
② 偏相関係数
③ 自己相関係数
④ 正準相関係数
⑤ 部分相関係数
解答のポイント
「相関係数」と名のつく概念の弁別ができている。
選択肢の解説
② 偏相関係数
⑤ 部分相関係数
そもそも「相関」とは、2つの変数がどのくらい一緒に変動するかを示す概念であり、2変数の直線相関が最も一般的(ピアソン)で、この場合、2変数の関係は直線であらわすことができます(一般的に「相関係数」といえば、ピアソンの積率相関係数を指すことが多いです)。

こちらがピアソン。名は元Carlであったが、のちにカール・マルクスに傾倒して自らKarlと変えた。
「2変数の直線相関」というのも少しわかりにくい表現かもしれませんが、実態はそれほど難しい話ではありません。
要は「片方が上がる(下がる)とき、もう片方はどうなるの?」ということであり、身長と体重で言えば「身長が上がれば、体重も上がる傾向にある」という片方が上がればもう片方も上がることを正の相関と呼び、気温とおでんの売り上げで言えば「気温が上がれば、おでんの売り上げは下がる」という片方が上がればもう片方が下がることを負の相関と呼ぶのです。
以下のように座標軸でプロットされることになりますね。
こうしたx軸とy軸を作り、各ケースのデータをプロットして、両変数間の関係を表したものを一般に「散布図」と呼び、相関係数を用いるときに使う図表と理解しておいてください。
これらを踏まえた上で、選択肢②の「偏相関係数」と選択肢⑤の「部分相関係数」を考えていきましょう。
「偏相関係数」と「部分相関係数」は、3つ以上の変数がある場合に、この中から取り出した2変数の相関係数になるのですが、単純な2変数の相関係数ではなく、第3の変数の影響を除外して考えた2変数間の相関係数のことを指します。
まずは「偏相関係数」について考えていきましょう(こちらのサイトの例がわかりやすかったので参考にしつつ述べていきます)。
「映画のスクリーン数」と「薬局の数」という2つの相関関係を見たとき、これらには正の相関がみられました。
映画館のスクリーン数が多いから薬局の出店数が増えるわけでも、薬局の数が多いから映画館のスクリーン数が増えるわけでもないので、この結果は奇妙に見えますよね。
このような場合には「第3の因子」の存在を考慮する必要があります。
この「第3の因子」として「人口数」が挙げられ、この因子は「映画のスクリーン数」および「薬局の数」とも強い正の相関があることが示されました(相関係数はそれぞれ0.85と0.98だった。相関では1が最大なので、相当高い数字である)。
ここで改めて「映画のスクリーン数」と「薬局の数」の相関関係を見ていくとき、「人口数」という第3の因子の影響を取り除いて考えないと、本当の相関関係を把握することができないことになります。
そこで、第3の因子の影響を除いた相関係数である「偏相関係数」を用いて相関関係を評価したところ、映画館のスクリーン数と薬局の数との相関は実はあまり強くないことが分かりました。
ここで挙げた映画館のスクリーン数と薬局の数のように、実際には相関関係がないのにあるように見える関係のことを「見かけ上の相関」「疑似相関」と呼びます。
このように3つ以上の変数がある場合、ある変数が他の変数間の相関に影響を与えているということが少なからずあります。
ですから、偏相関係数を出すことによって、純粋に見たい変数同士の相関関係を算出することができるということですね。
偏相関係数は量的変数同士のデータで利用する指標であり、使いどころとしては、重回帰分析で独立変数と従属変数の影響関係の妥当性を確認するために参照されることが多いですね。
続いて、部分相関係数についても考えていきましょう。
先述の通り、こちらも「第3の変数の影響を除外して考えた2変数間の相関係数のこと」を指します。
そして、部分相関係数は、相関を求める2つの変数のうち、1つの変数が第3の変数の影響を除いたものであるとき、その相関係数を部分相関係数と呼びます。
これだけだと、先の偏相関係数との違いが分かりづらいと思いますので、以下の図を見て見ましょう。
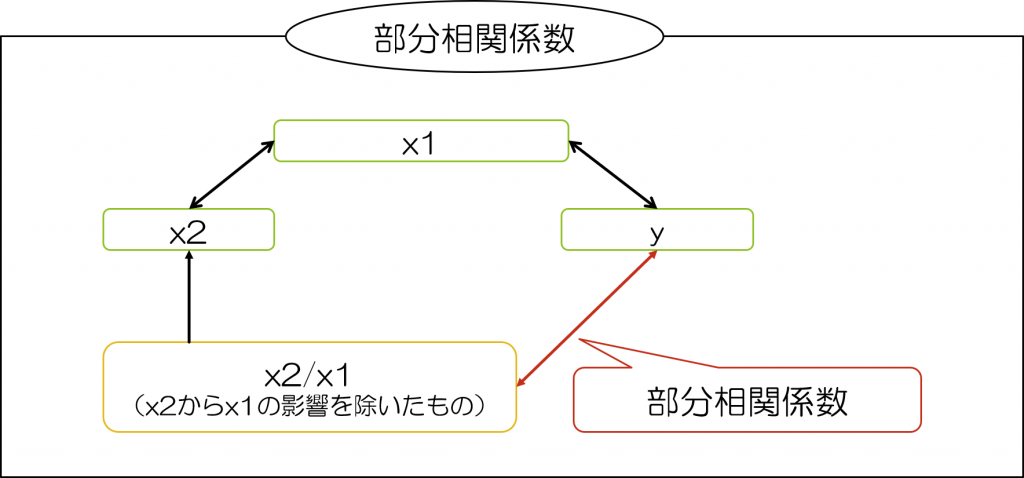
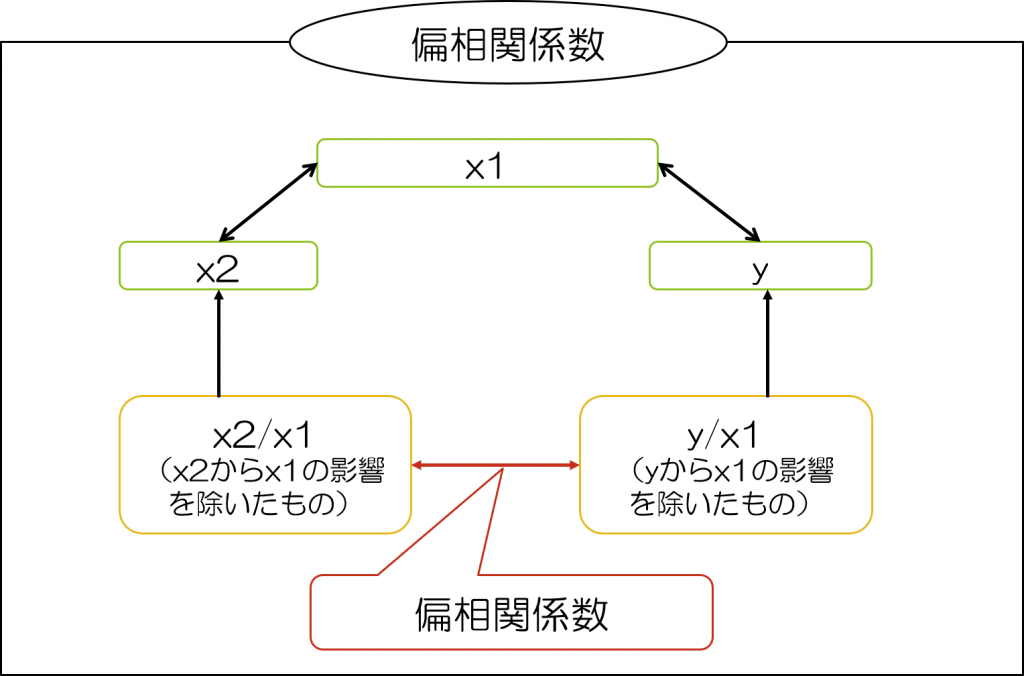
このように見てみると、両者の違いが分かりやすいと思います。
つまり、部分相関係数では「相関を求める2つの変数のうち、1つの変数が第3の変数の影響を除いたものであるとき、その相関係数を部分相関係数と呼ぶ」のに対して、偏相関係数では「相関係数を求める2つの変数のそれぞれから、共通の第3の変数の影響を除くとき、その相関係数を偏相関係数と呼ぶ」となるわけです。
部分相関係数が利用される最も重要な場面は、重回帰分析における独立変数の選択する時です。
例えば、従属変数yに対して、最初の独立変数としてzが選ばれており、第2の独立変数としてxを追加すべきかどうかを検討する際には、yとx|z(xのうちzに含まれていない情報)の部分相関係数を考えて決定します。
こちらも偏相関係数と同様、量的変数同士のデータで利用する指標となります。
以上を踏まえると、本問の「相関関係を求める2つの変数それぞれから、共通の第3の変数の影響を除いて求められる相関係数」とは、偏相関係数であることがわかりますね。
よって、選択肢⑤が不適切と判断でき、選択肢②が適切と判断できます。
① 重相関係数
まずは重回帰分析の解説から入っていきましょう。
重回帰分析とは、従属変数(=目的変数or基準変数)のばらつきを、いくつかの独立変数(=説明変数)によって説明・予測するための統計的手法のことで、一つの従属変数に対して一つの独立変数によって説明・予測するのを「単回帰分析」と呼び、独立変数が複数ある場合を「重回帰分析」と呼びます。
例えば、身長を体重という一つの説明変数から予測するのは単回帰分析であるのに対して、重回帰分析は身長を体重、年齢、性別など複数の説明変数から予測します。
上記のような線を「回帰」と呼び、重回帰分析(単回帰分析も)は、こうした回帰直線を求めるので「重回帰分析・単回帰分析」という名が付いています(重や単は独立変数(説明変数)が複数か単数かで分けられるということです)。
重回帰分析を使用できるのは、複数の説明変数によって1つの目的変数を説明しようというモデルにおいてです。
この時、説明変数相互の相関関係にも考慮し、その影響を取り除いて、各説明変数の純粋な影響を取り出すのが狙いになります(以下のようなイメージになります)。

実際には、説明変数によって基準変数(目的変数)に与える影響の大小があったり、説明変数以外に基準変数に影響を与える要因(これを誤差と呼びます)があります。
数式で述べれば、「目的変数(の予測値)=b1×説明変数1+b2×説明変数2+b3×説明変数3+b4×説明変数4」という形になり(切片のcとかあるけど、それはさておき)、こうした目的変数の予測値に誤差を足したものが実際の数値になるわけです。
当然、誤差が大きいほど目的変数の値にズレが出ますから、説明変数で説明できない領域が大きくなってしまうので好ましくなく、誤差を小さくすることで説明変数によって予測できる割合が高まるわけですね。
この重回帰分析において、必ず理解しておかねばならないのが重相関係数と標準偏回帰係数についてです。
「重相関係数」とは「いくつかの説明変数全体が従属変数に与える影響を示した値」であり、説明変数全体での影響の大きさを示す指標ですから、説明変数が何個あろうが算出されるのは1つだけです(一般にRで表され、普通の相関係数(r)は区別のために「単純相関係数」や「単相関係数」と呼ばれます)。
重相関係数を二乗したものが「決定係数」であり、これは「目的変数の予測値が、実際の目的変数の値とどのくらい一致しているかを表している指標(単純に言えば、決定係数が0.7ならその説明変数で従属変数の70%を説明できる)」というものです。
「標準偏回帰係数」とは、他の変数の影響を取り除いた時の、各説明変数の影響の大きさと向きを表します(要は、複数ある説明変数それぞれ単体での目的変数への影響を表したもの。βと表記される)。
これらを踏まえると、本問の「相関関係を求める2つの変数それぞれから、共通の第3の変数の影響を除いて求められる相関係数」に重相関係数は合致しないことがわかりますね。
以上より、選択肢①は不適切と判断できます。
④ 正準相関係数
重回帰分析は1つの従属変数のばらつきを、複数の独立変数によって説明・予測するための統計的手法でしたが、これに対して、複数の従属変数に対して、複数の独立変数が影響することを調べる手法を正準相関分析と呼びます。
例えば、体力測定を行い、身長・体重・上肢長・下肢長の変数群(独立変数群)が、握力・背筋力・垂直跳びの変数群(従属変数群)にどのように関係するか知りたいときに、いくつかの方法が考えられます。
その一つは、2種類のグループについて総当りで相関係数を求め、それらを総合的に評価する方法です。
上記の例の場合、4×3=12種類の単相関係数が求められることになります。
そして同じグループの臨床検査値間には相関があることを考慮した上で、これら12種類の単相関係数を検討し、相関関係を総合的に評価する必要がありますが、これは正直かなり面倒で難しい作業になります。
もう一つの方法は、重相関係数を利用するというやり方です。
重相関係数は、一つの項目と複数の項目の間の相関性を表す指標ですから、2種類のグループのうち数が少ない方の項目の一つひとつについて、もう一方のグループとの重相関係数を求めることによって評価すべき相関係数の数を減らすことができます。
しかし、この方法でも、独立変数同士の相関は山勘で評価することになりますから、これでは何となく中途半端になってしまいます。
そこで用いるのが正準相関係数になります。
こちらは言わば「グループ間の相関」について考える方法であり、2つのグループの相関関係を1つの相関係数で要約できます。
そのようなグループ間の相関のことを正準相関といい、正準相関の程度を表す指標のことを正準相関係数と呼びます。
この正準相関係数を求める手法のことを「正準相関分析」と呼び、これは重相関係数と重相関分析を拡張した手法に相当します。
各方法のイメージ図は以下のような感じです。

心理学分野では、心理的因子を複数のアンケート項目によって評価し、それらの心理的因子がお互いにどのように関連しているかを検討することがあります。
すなわち、複数の指標を総合して検討することが多く、その意味で正準相関分析は心理学分野で活用されやすい統計手法と言えます。
これらを踏まえると、本問の「相関関係を求める2つの変数それぞれから、共通の第3の変数の影響を除いて求められる相関係数」に正準相関係数は合致しないことがわかりますね。
よって、選択肢④は不適切と判断できます。
③ 自己相関係数
自己相関係数は、ある時点のデータとその一定の時点前のデータとの間の関連性を測る指標です。
1つの時系列データを対象として、少しずつ時間をずらして相関を求めることになり、自分自身の過去のデータとどのくらい類似しているかを調べられるという「自分自身のラグ(元データからずらす時間の度合いを表す指標)だけから相関を求める」という特徴を踏まえて自己相関と呼ばれています。
例えば、過去の一定の時点前のデータと現在のデータが強く関連している場合には「自己相関係数」は高い値を示しますが、逆に、過去のデータと現在のデータに関連性がない場合は「自己相関係数」は低い値を示すことになるわけです(自己相関係数は-1から1の範囲を取り、1に近いほど強い正の自己相関があり、-1に近いほど強い負の自己相関がある。また、0に近い場合は自己相関がほとんどないことを示す)。
その特性上、気温データの分析や、身近なところだと電気代使用量の推移などを見るときに用いられることが多いですね。
自己相関係数ある場合は「今月の値には先月の値が影響する」「先月の値には先々月の値が影響する」≒「今月の値には先々月の値が関係する」というような推移関係が成立することになります(今月と先々月を直接的に調べているのではない)。
こちらのサイトなどがわかりやすい説明をしていますね。
これらを踏まえると、本問の「相関関係を求める2つの変数それぞれから、共通の第3の変数の影響を除いて求められる相関係数」に自己相関係数は合致しないことがわかりますね。
よって、選択肢③は不適切と判断できます。