データ分布の特徴を示す指標のうち、外れ値の影響を受けにくいものを選択する問題です。
過去問でも解説したことのある内容でしたね(平均年収の代表値として、どれが適切かみたいな話でよく出てくる話題です)。
問82 データ分布の特徴を表す指標のうち、外れ値の影響を受けにくいものとして、最も適切なものを1つ選べ。
① 範囲
② 分散
③ 中央値
④ 平均値
⑤ 標準偏差
解答のポイント
各指標の特徴を把握している。
選択肢の解説
③ 中央値
④ 平均値
選択肢③の中央値は、よく使われる代表値の一つです。
Median(中央値:Me)は、データを大きさの順に並べたときに、ちょうど真ん中に位置する値です。
データが偶数の場合は、真ん中にある2つの数字の平均値を算出し、それを中央値とします。
また、選択肢④の平均値もよく使われる代表値であり、データを全て足して、データ数で割ったものになります。
一般に、平均値の方が全てのデータを結果に反映させているため、中央値よりも平均値の方が「情報をフルに利用している指標」と見なすことができます。
ただし、平均値に偏りがある場合には、中央値の方が有効な代表値になることもあります。
例えば、ある会社の社員9名の年収が400万円として、社長の年収が6400万円だとすると、その会社の平均年収は1000万円となりますが、これはその会社の実態を表しているとは言えないですよね。
このように、極端な外れ値が存在したり分布に大きな偏りがある場合、平均値のように「すべての情報をフルに利用している」という特徴が足を引っ張り、実態の姿から遠ざかってしまうということになってしまうわけです。
こういう状況においては、大きすぎる値や小さすぎる値がいくつか含まれていたとしても(要するに外れ値があったとしても)、ほとんど影響を受けない中央値が有効になります。
先の例だと、年収の中央値は400万円になりますから、こちらの方が実態に近く、例えば会社を選ぶ際の有効な指標になりそうですね。
以上のように、平均値はよりデータの情報を活用した代表値でありますが、その特性故に極端に小さすぎたり大きすぎたりする値(=外れ値)に足を引っ張られやすく、それによって実態から遠ざかってしまう値が算出されるリスクが大きいと言えます。
これに対して、中央値は「大きい順に並べて真ん中を取る」という単純な構造であるが故に、端っこの数字が何であっても影響を受けない(=外れ値を度外視する)という特徴があり、それ故に活用しやすい状況が存在するということになります。
しかし、データによっては「端っこの数字も含めて考えた方が良いもの」もありますから、必ずしも中央値があらゆる状況で平均値に勝るというわけではありません。
あくまでも、現代社会の「世界の富の9割を、1割の人間が占有している」などのようなデータ(=外れ値が存在している。こういう状況での「平均値」は当てにならず、「中央値」が実態を表す)のときに利用価値が上がりやすい代表値が「中央値」ということができますね。
以上より、選択肢④は不適切と判断でき、選択肢③が適切と判断できます。
① 範囲
② 分散
⑤ 標準偏差
これらは散布度という「データの散らばりの程度」の特徴を表す指標になります。
心理学研究のように、測定される対象が人であり、ある変数に関して各対象から1つずつデータが得られている一般的なケースでは、散布度の大きさは個人差の大きさに対応します。
ですから、例えば、ある条件のもとで得られたある変数についてのデータの散布度が他の条件のもとで得られた同じ変数についてのデータの散布度に比べて小さいということは、前者の条件下では人の反応が画一化されやすいことを意味していると解釈できると思います。
また、同一個人に同じ条件下で複数回の測定を繰り返したデータの散布度が小さいことは、その個人の反応が安定していることを表わしているでしょう。
そして、代表値として平均値か中央値を用いている場合にそのデータの散布度が小さいということは、多くのデータが代表値の近くに集中しており、平均値や中央値を用いて「データの値は普通〇〇くらいです」と記述することの信頼性が高い(そのような記述が、多くの対象の実状からかけ離れたものになっていない)ことを意味しています。
以下では、挙げた選択肢である「範囲」と「分散」「標準偏差」について述べていきます。
選択肢①の範囲は、データの「散らばり」を調べるもっとも手軽な方法の一つです。
範囲はデータの分布の幅を示すもので、散らばり具合の幅が大きいか、小さいかを示す指標であり、具体的にはデータの中の最大値と最小値の差で求めます。
「範囲」は、計算は簡単ではあるのですが、外れ値の影響を直接的に受ける偶然性の高いものであると共に、データ数が多いほど大きな値になる確率が高くなるため、活用度が高い指標とは言えず、あくまでも散布度についての大雑把な目安に過ぎないという特徴があります(前選択肢解説の例では6000万円になってしまい、実態を表しているとは言えませんね)。
選択肢②の「分散」および選択肢⑤の「標準偏差」についてはまとめて解説していきましょう。
ネジの直径を例にとると、ネジの直径は大きすぎても小さすぎてもネジとして使えないので、上限と下限の規格値が決められています。
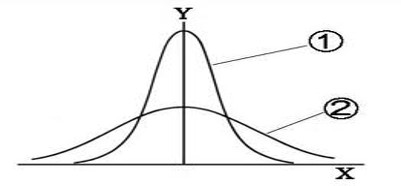
上記の図で言うと、②だと両端が使えなくなるので不良品が多くなりますが、①だとより使えるネジが多いということになりますね。
分布のバラツキが大きすぎると、検査に合格しない不良品が多く出ることになりますから、できるだけ尖った形の分布(①)の方がものづくりをする上では好ましいわけです。
このバラツキ具合を示すような代表値があると便利なわけですが、それが「分散」「標準偏差」ということになります。
上記の図の、①の尖った分布と②の平たい分布を比較すると、平たい分布ではY軸(平均値;m)から線までの距離が遠く離れているのがわかるはずです(下の図のような感じ)。
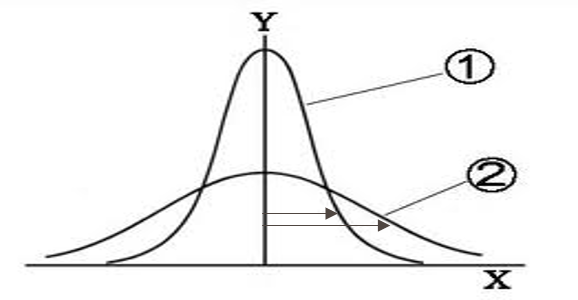
平均値(Y軸:m)から、各データとの距離を測り(各データ‐m)、それを総合したら、平たい分布(バラつきのある分布、外れ値の多い分布、上記で言う②)の方の値が大きくなるのがわかると思います。
この「各データ‐m」を統計では「偏差」と呼びますが、この偏差を全て足すと外れ値の多い分布の方が大きな数字になります。
ただ、このまま「各データ‐m」だけをやっていると、偏差のプラスとマイナスが打ち消し合い、総和はゼロになってしまうので、そこで偏差の符号を消すために二乗にして足していきます(二乗にすることで「差が際立つ」というメリットもある)。
しかし、この「(各データ‐m)の二乗の総和」では、データの数によって影響を受けてしまうので(データが大きいほど、出てくる数値も大きくなってしまう)、データの数で割ることになります。

これを計算式に落とし込んだものが上記になりますが、この「(各データ‐m)の二乗の総和をデータ数で割ったもの」を「分散」と呼ぶのです。
そして、この「分散」に平方根を付けたものが「標準偏差」となるのです。
これが「分散」や「標準偏差」のざっとした算出法になるわけですが、上記の説明にもあったように、分布がなだらかで外れ値が多く存在するような場合、分散や標準偏差が大きくなってしまい、かなり影響を受けることがわかると思います。
外れ値とは、平均値から大きく外れることになりますから「各データ‐m」という箇所で大きな数字をたたき出してしまい、それが分散や標準偏差の数値の大きさにつながるということです。
具体的に、A(2、3、4)、B(1、3、5)、C(3、3、3)という3種類のデータの標準偏差を算出すると、AのSD=0.8、BのSD=1.6、CのSD=0ということになります。
このように、標準偏差は個々の値と平均値の差(偏差)の二乗の平均(ここまでが「分散」)の平方根をとった値ですから、大雑把に言えば「個々の値が平均値から離れている程度についての標準的な値」ということになります。
外れ値についても、平均値との差を算出して計算に組み込んでいくので、当然、外れ値の影響が分散・標準偏差共に大きくなるのです。
以上より、選択肢①、選択肢②および選択肢⑤は不適切と判断できます。