重回帰分析の概念に関する問題です。
統計の問題では、計算させるような問題は絶対に出題しませんが、このように「その分析が何を行っているか」「どういう条件下で行われるか」についての理解が求められますね。
問6 重回帰分析において、説明変数間の相関の絶対値が大きく、偏回帰係数の推定が不安定となる状態を説明する概念として、正しいものを1つ選べ。
① 一致性
② 共通性
③ 独自性
④ 不偏性
⑤ 多重共線性
関連する過去問
解答のポイント
重回帰分析を成立させるための前提条件を把握している。
選択肢の解説
⑤ 多重共線性
まずは重回帰分析の解説から入っていきましょう。
重回帰分析とは、従属変数(=目的変数or基準変数)のばらつきを、いくつかの独立変数(=説明変数)によって説明・予測するための統計的手法のことで、一つの従属変数に対して一つの独立変数によって説明・予測するのを「単回帰分析」と呼び、独立変数が複数ある場合を「重回帰分析」と呼びます。
例えば、身長を体重という一つの説明変数から予測するのは単回帰分析であるのに対して、重回帰分析は身長を体重、年齢、性別など複数の説明変数から予測します。
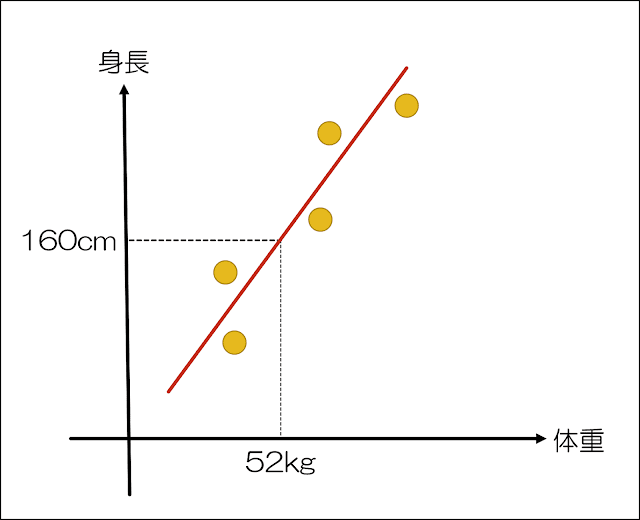
上記のような線を「回帰」と呼び、重回帰分析(単回帰分析も)は、こうした回帰直線を求めるので「重回帰分析・単回帰分析」という名が付いています(重や単は独立変数(説明変数)が複数か単数かで分けられるということです)。
重回帰分析を使用できるのは、複数の説明変数によって1つの目的変数を説明しようというモデルにおいてです。
この時、説明変数相互の相関関係にも考慮し、その影響を取り除いて、各説明変数の純粋な影響を取り出すのが狙いになります(以下のようなイメージになります)。

実際には、説明変数によって基準変数(目的変数)に与える影響の大小があったり、説明変数以外に基準変数に影響を与える要因(これを誤差と呼びます)があります。
数式で述べれば、「目的変数(の予測値)=b1×説明変数1+b2×説明変数2+b3×説明変数3+b4×説明変数4」という形になり(切片のcとかあるけど、それはさておき)、こうした目的変数の予測値に誤差を足したものが実際の数値になるわけです。
当然、誤差が大きいほど目的変数の値にズレが出ますから、説明変数で説明できない領域が大きくなってしまうので好ましくなく、誤差を小さくすることで説明変数によって予測できる割合が高まるわけですね。
この重回帰分析において、必ず理解しておかねばならないのが重相関係数と標準偏回帰係数についてです。
「重相関係数」とは「いくつかの説明変数全体が従属変数に与える影響を示した値」であり、説明変数全体での影響の大きさを示す指標ですから、説明変数が何個あろうが算出されるのは1つだけです(一般にRで表され、普通の相関係数(r)は区別のために「単純相関係数」や「単相関係数」と呼ばれます)。
重相関係数を二乗したものが「決定係数」であり、これは「目的変数の予測値が、実際の目的変数の値とどのくらい一致しているかを表している指標(単純に言えば、決定係数が0.7ならその説明変数で従属変数の70%を説明できる)」というものです。
「標準偏回帰係数」とは、他の変数の影響を取り除いた時の、各説明変数の影響の大きさと向きを表します(要は、複数ある説明変数それぞれ単体での目的変数への影響を表したもの。βと表記される)。
ここまでが重回帰分析の大まかな説明になります。
これらを踏まえ、本問の各選択肢の解説に入っていきましょう。
この重回帰分析には「この分析をやるからには、これは守ってくださいよー」というルールがあり、それが「説明変数間の相関は無い、もしくは、あってもごく僅かである」というものです。
説明変数間の相関が高いと偏回帰係数の推定が不安定になりやすく(偏回帰係数は他の説明変数の影響を取り除かなきゃいけないのに、相関が強かったらそれが難しくなる)、得られた回帰直線の当てはまりが良くないという問題が生じますが、この現象を「多重共線性」と呼び、結果の解釈が困難にさせます。
この原因として、相関係数が大きいと偏相関係数の推定値の分散が大きくなり、データを取るごとに偏回帰係数の値が大きく変化することによります。
この説明でわかりにくい人も多いと思いますので、以下の図を見てもらいましょう。
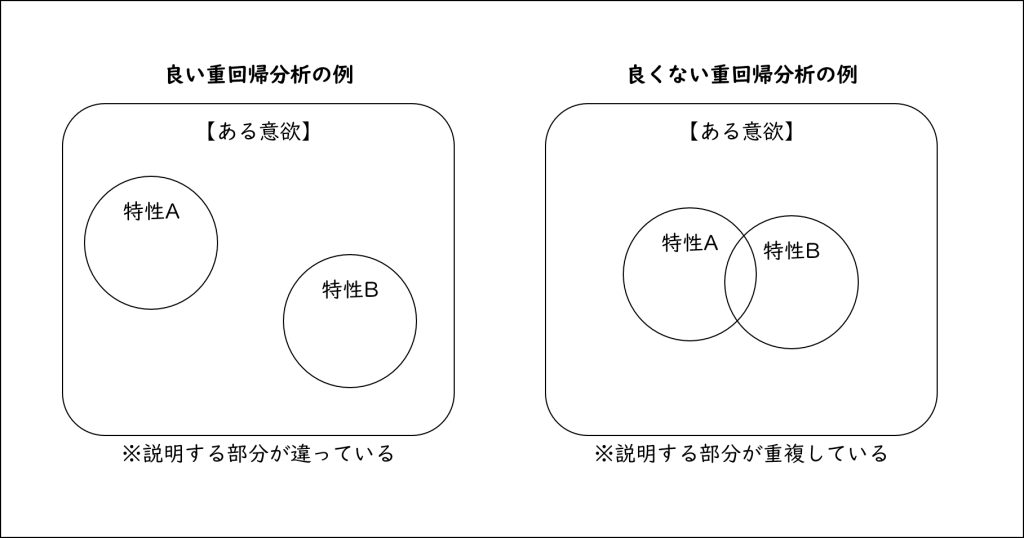
上記のように、ある意欲について検証する際に、特性①と特性②が重なっていると、同じ部分を重複して二度も説明してしまうということが起こります(=回帰の統計量が影響される)。
重回帰分析に持ち込む変数は、相互に説明する部分が違っていることが大前提となっているのです。
変数選択に方法を上手に利用することで、多重共線性の問題を避けることが可能です。
一般に、多重共線性の問題は変数が多くなれば多くなるほど心配されるので(当然ですよね)、多くの変数があるとき、似たような変数同士は一つにまとめ、異なる変数同士は全く独立に分離するという対処を取ることになります。
このように、重回帰分析において「説明変数間の相関の絶対値が大きく、偏回帰係数の推定が不安定となる状態を説明する概念」とは、多重共線性のことであるとわかりますね。
よって、選択肢⑤が正しいと判断できます。
① 一致性
④ 不偏性
これらは母集団を推定するときの「推定値の望ましさ」を表す指標になります。
統計では、母集団から取り出した一部の標本から母集団の特徴を推測することになります。
例えば、缶詰工場のすべての缶詰を開けて不良品の有無を確かめるというわけにはいかないから、一部を取り出して開封して問題が無ければ「一部の缶詰(標本)に問題がなかったから、すべての缶詰(母集団)に問題がないと見なす」ということになるわけですね。
当然ながら、一部の標本から母集団を推定する場合には、その推定ができる限り正確であることが求められます(じゃないと、缶詰に異物が混ざる可能性が高まるからね)。
母集団を推定する方法はいくつかありますが(最小二乗法や最尤推定法など)、こうして示された推定値の良さ(正確さ)を表す指標として「一致性」「不偏性」「有効性」があります。
まず「一致性」ですが、母集団から取り出す標本の数が多ければ多いほど、その標本が示す数値は母集団のそれと近くなるのは自明ですよね。
このように、標本数が大きくなれば、推定量がだんだんと真の母集団(パラメータ)に近づく性質を「一致性」と言います。
上記の例で言えば、工場で作っている缶詰の開く数を増やすほどに、母集団(その工場で作っている缶詰全部)の不良品の割合を正確に割り出せるわけですね。
言われてみれば当たり前ですが、そういう性質のことを「一致性」と呼ぶのです。
続いて「不偏性」ですが、これを一言でいえば「その推定量が平均的に過大にも過小にも母数を推定しておらず、推定量の期待値が母数に等しい」という性質です(より具体的には、標本数に依存せず、計算した推定値は平均的に見てバイアスがないという意味)。
標本からの推定量を元に母集団を推測するとき、その推測が真の母集団から大きく外れてしまっては意味がありません。
言い換えると、推定量の期待値が母集団(パラメータ)に一致する必要があり、期待値が真のパラメータになることを「不偏性」と呼ぶのです。
例えば、会社全体のオシャレ度を測定するのに、その会社の広報部の人たちを標本として推定値を出していくことにします。
その際、広報部の人たちを標本とすると実際の会社全体のオシャレ度よりも高く算出されることになってしまったとすると、この「広報部という標本」から得られた推定値は真の値の周りを散布していない(会社全体のオシャレ度の周辺をウヨウヨしていない)ので望ましい推定量とは言えず、いくら標本サイズを変えたとしても(広報部からの標本数を増やしたり減らしたりしても)推定値の平均は真の値と一致しないことになりますね。
最後に「有効性」ですが、有効性があるとは「ある母数の推定量との比較において、その推定量の分散がもっとも小さいこと」を意味します。
より具体的には、その推定量が他の推定量と比較してもっとも精度がよいと考えられるだろう、という意味になります。
以上より、一致性や不偏性は「重回帰分析において、説明変数間の相関の絶対値が大きく、偏回帰係数の推定が不安定となる状態を説明する概念」ではないことがわかりますね。
よって、選択肢①および選択肢④は誤りと判断できます。
② 共通性
③ 独自性
これらは因子分析で用いられる概念になりますから、まず因子分析の概要について述べていきましょう。
心理学では通常、観測されたデータから目に見えない要因(因子)について議論することが多く、それを検討するためによく用いられるものとして因子分析が広く用いられています。
つまり、因子分析とは「きっと世の中に存在するに違いない「データの背後に潜む説明変数(独立変数)」を見つけ出す分析手法」と言えます。
例えば、国語、数学、理科、社会、英語の5教科があるとして、この5教科の背景にある共通因子を見つけるのが「因子分析」になります。
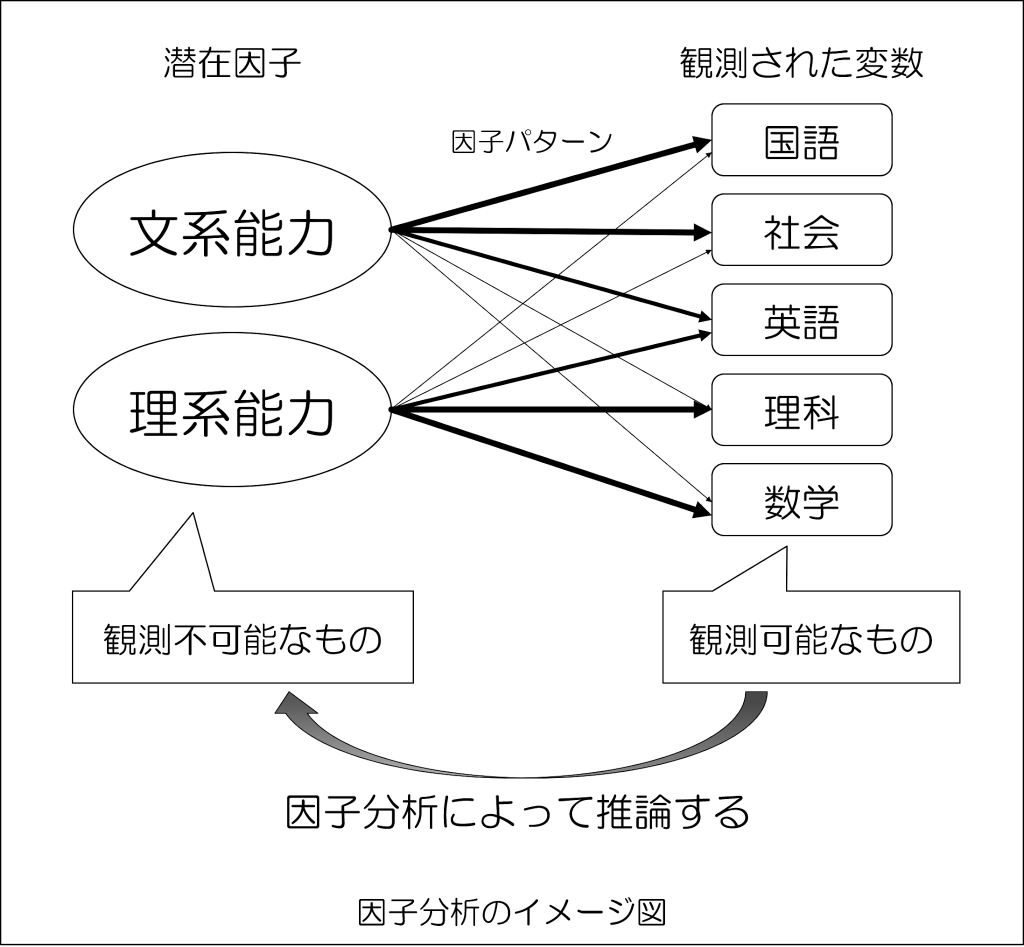
観測された変数である5教科の得点は、共通(潜在)因子(文系能力・理系能力)から影響を受けていることになり、上記の矢印の太さが影響の度合いである「因子負荷量」の大小を表現していると考えてください。
ここで挙げた選択肢の「共通性」とは、各観測変数の分散のうち、共通因子の変動によって説明される部分の割合のことを指します。
わかりにくい人も多いと思うので、上記の例で平たく言えば、示された「文系能力」「理系能力」によって、観測変数(国語、社会、英語、理科、数学)というものを説明できているほど「共通性が高い」と言えるわけです(共通因子と観測変数が「共通している」というイメージで良いかなと思います)。
つまり、共通性が大きいほど(最大で1)その項目は因子の影響を強く受けているということができ(分析で抽出された因子によってよく説明できている)、小さいほど因子とは関係ない項目だということができます。
上記を言い換えれば、どんなデータであっても因子に支配されずに独自に動く部分があるわけですが、この独自に動く部分を「共通性」に対して「独自性」と呼びます(つまり、「1-共通性」で導かれる)。
独自性の大きい項目は因子抽出に向かないので、その項目を除外した上で再度因子分析を行っていくことがあります。
以上より、共通性や独自性は「重回帰分析において、説明変数間の相関の絶対値が大きく、偏回帰係数の推定が不安定となる状態を説明する概念」ではないことがわかりますね。
よって、選択肢②および選択肢③は誤りと判断できます。