2×2のクロス集計表に関する問題です。
実は過去問とのクロスオーバーがある問題ですから、その問題も含めて復習しておくと良いでしょう。
問82 2×2のクロス集計表における2変数間の関連性を示す指標として、最も適切なものを1つ選べ。
① 偏相関係数
② 順位相関係数
③ 積率相関係数
④ 部分相関係数
⑤ 四分点相関係数
解答のポイント
2つの変数の関係を分析する方法について概観できている。
「公認心理師 2018追加-82」を明確に理解できている。
選択肢の解説
本問では「2つの変数の間の関係を数値で記述する方法やその有意性の検定法」に関して問われています。
簡単に言えば「2つの変数の関係を分析する方法」について問われているわけですね。
具体的には「ピアソンの積率相関係数」「連関係数」「順位相関係数」などについてです。
この順番で解説していきますね。
ちなみに過去問の「公認心理師 2018追加-82」で「クロス集計表の連関の検定で利用される確率分布として正しいものを選べ」という出題があり、この中の解説でほぼ本問の解説になるような記述をしていますね。
唯一「φ係数=四分点相関係数」と表記していないので、その辺が不十分だったくらいですが、それでも過去問をしっかりやっておけば何とか攻略できる部類の問題だったと言えるでしょう(統計は理解の得手不得手が出やすい領域ですから、その辺で苦手な人はいるかもしれませんが)。
③ 積率相関係数
① 偏相関係数
④ 部分相関係数
これらの選択肢に関してはまとめて解説していった方がわかりやすいと思います。
そもそも「相関」とは、2つの変数がどのくらい一緒に変動するかを示す概念であり、2変数の直線相関が最も一般的(ピアソン)で、この場合、2変数の関係は直線であらわすことができます(一般的に「相関係数」といえば、ピアソンの積率相関係数を指すことが多いです)。

こちらがピアソン。名は元Carlであったが、のちにカール・マルクスに傾倒して自らKarlと変えた。
「2変数の直線相関」というのも少しわかりにくい表現かもしれませんが、実態はそれほど難しい話ではありません。
要は「片方が上がる(下がる)とき、もう片方はどうなるの?」ということであり、身長と体重で言えば「身長が上がれば、体重も上がる傾向にある」という片方が上がればもう片方も上がることを正の相関と呼び、気温とおでんの売り上げで言えば「気温が上がれば、おでんの売り上げは下がる」という片方が上がればもう片方が下がることを負の相関と呼ぶのです。
以下のように座標軸でプロットされることになりますね。
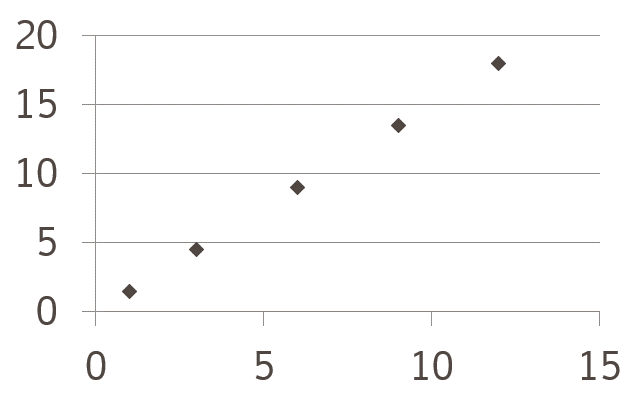
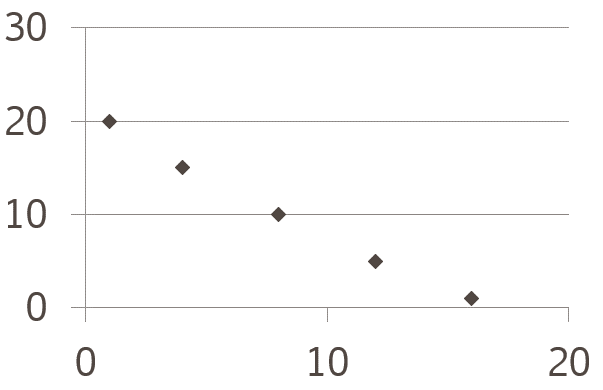
こうしたx軸とy軸を作り、各ケースのデータをプロットして、両変数間の関係を表したものを一般に「散布図」と呼び、相関係数を用いるときに使う図表と理解しておいてください。
この「散布図」が本問の「クロス集計表」に対応する考え方ですから、しっかりと押さえておきましょう。
なお、こうした散布図にプロットすることになる以前の話ですが、ピアソンの積率相関係数を用いるときには「2変数の関係は直線であらわすことができる」わけですから、当然「量的変数と量的変数の関係について考える場合」に用いられることになります。
この点も、「2×2のクロス集計表における2変数間の関連性」と対応する部分ですから、しっかりと押さえておくようにしましょう(後述しますが、本問は「質的変数と質的変数の関係について考える」という状況なんです)。
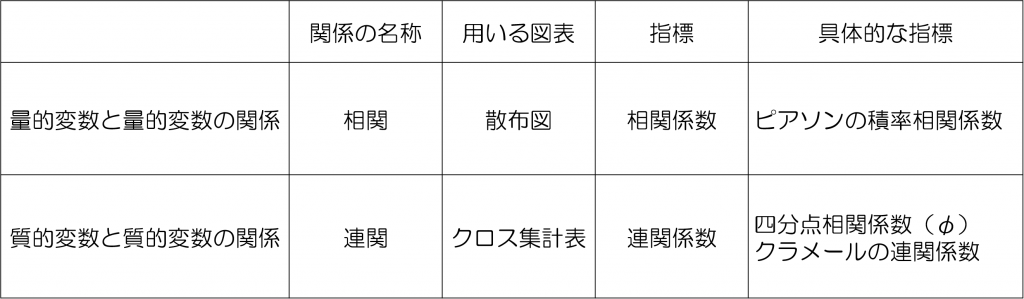
詳しくは選択肢⑤の解説も見てほしいのですが、積率相関係数と本問で示されている内容の対比を示すと上記のようになります。
(ピアソンの)積率相関係数が量的変数同士の関係であること、その場合は散布図を用いることなどを踏まえれば、選択肢③は真っ先に除外することができると言えますね。
さて、上記が「積率相関係数」に関する概要ですが、この時点で選択肢③は外すことができると理解できるだろうと思います(選択肢⑤の解説を読むとよりわかりやすいはずです)。
続いて、選択肢①と選択肢④についても考えてみましょう。
「偏相関係数」と「部分相関係数」は、3つ以上の変数がある場合に、この中から取り出した2変数の相関係数になるのですが、単純な2変数の相関係数ではなく、第3の変数の影響を除外して考えた2変数間の相関係数のことを指します。
まずは「偏相関係数」について考えていきましょう(こちらのサイトの例がわかりやすかったので参考にしつつ述べていきます)。
「映画のスクリーン数」と「薬局の数」という2つの相関関係を見たとき、これらには正の相関がみられました。
映画館のスクリーン数が多いから薬局の出店数が増えるわけでも、薬局の数が多いから映画館のスクリーン数が増えるわけでもないので、この結果は奇妙に見えますよね。
このような場合には「第3の因子」の存在を考慮する必要があります。
この「第3の因子」として「人口数」が挙げられ、この因子は「映画のスクリーン数」および「薬局の数」とも強い正の相関があることが示されました(相関係数はそれぞれ0.85と0.98だった。相関では1が最大なので、相当高い数字である)。
ここで改めて「映画のスクリーン数」と「薬局の数」の相関関係を見ていくとき、「人口数」という第3の因子の影響を取り除いて考えないと、本当の相関関係を把握することができないことになります。
そこで、第3の因子の影響を除いた相関係数である「偏相関係数」を用いて相関関係を評価したところ、映画館のスクリーン数と薬局の数との相関は実はあまり強くないことが分かりました。
ここで挙げた映画館のスクリーン数と薬局の数のように、実際には相関関係がないのにあるように見える関係のことを「見かけ上の相関」「疑似相関」と呼びます。
このように3つ以上の変数がある場合、ある変数が他の変数間の相関に影響を与えているということが少なからずあります。
ですから、偏相関係数を出すことによって、純粋に見たい変数同士の相関関係を算出することができるということですね。
偏相関係数は量的変数同士のデータで利用する指標であり、使いどころとしては、重回帰分析で独立変数と従属変数の影響関係の妥当性を確認するために参照されることが多いですね。
なお、偏相関係数に関しては「臨床心理士 平成21年 問題39 B」に出題があります。
「3変数で偏相関を求めると、一つの偏相関係数が得られる」に対して正誤判断をする選択肢になっており、答えは「×」になりますね(正しくは二つの偏相関係数が得られる)。
余力のある方はやってみると良いでしょう。
続いて、部分相関係数についても考えていきましょう。
先述の通り、こちらも「第3の変数の影響を除外して考えた2変数間の相関係数のこと」を指します。
そして、部分相関係数は、相関を求める2つの変数のうち、1つの変数が第3の変数の影響を除いたものであるとき、その相関係数を部分相関係数と呼びます。
これだけだと、先の偏相関係数との違いが分かりづらいと思いますので、以下の図を見て見ましょう。
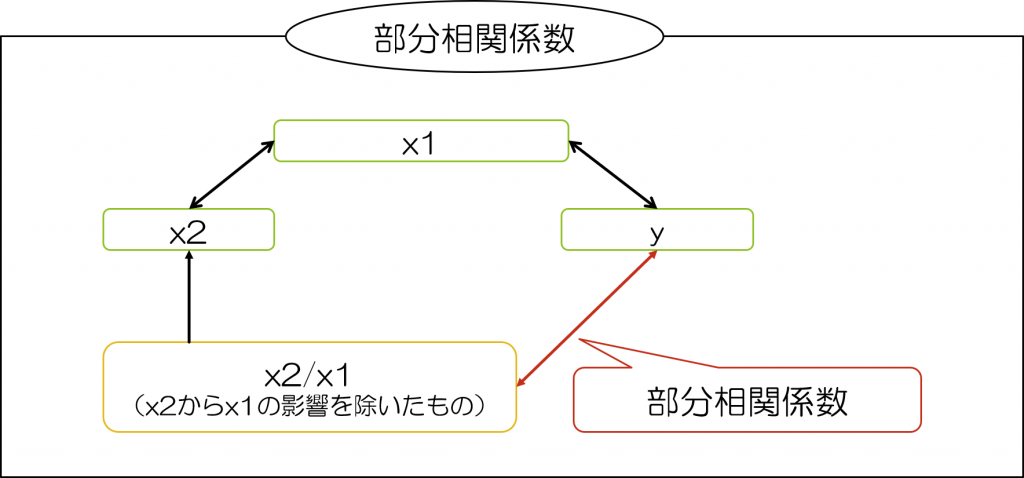
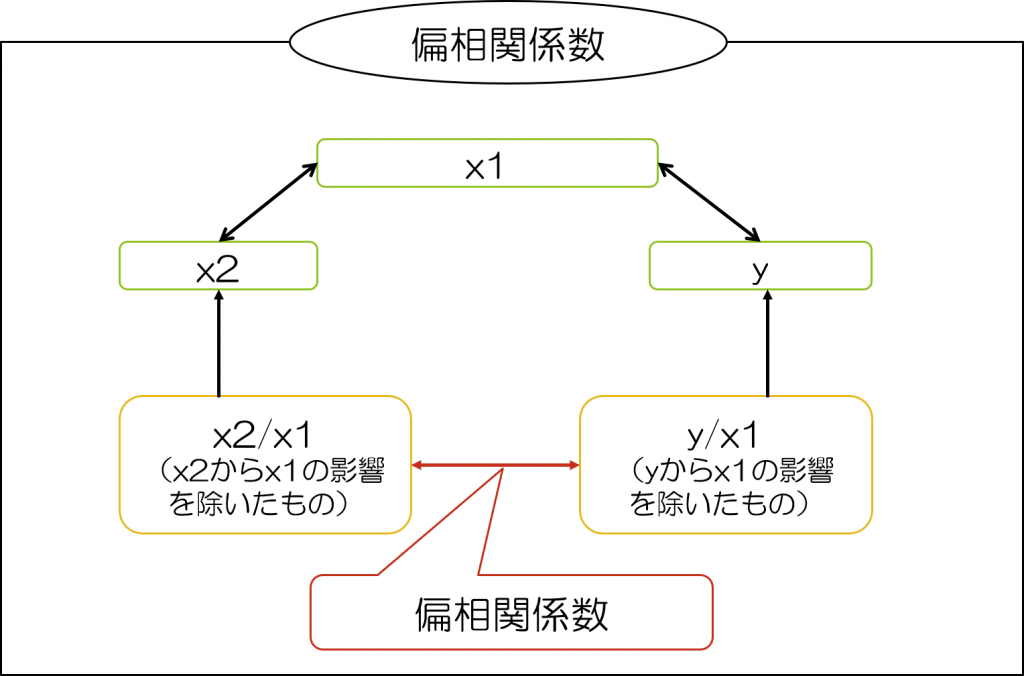
このように見てみると、両者の違いが分かりやすいと思います。
つまり、部分相関係数では「相関を求める2つの変数のうち、1つの変数が第3の変数の影響を除いたものであるとき、その相関係数を部分相関係数と呼ぶ」のに対して、偏相関係数では「相関係数を求める2つの変数のそれぞれから、共通の第3の変数の影響を除くとき、その相関係数を偏相関係数と呼ぶ」となるわけです。
部分相関係数が利用される最も重要な場面は、重回帰分析における独立変数の選択する時です。
例えば、従属変数yに対して、最初の独立変数としてzが選ばれており、第2の独立変数としてxを追加すべきかどうかを検討する際には、yとx|z(xのうちzに含まれていない情報)の部分相関係数を考えて決定します。
こちらも偏相関係数と同様、量的変数同士のデータで利用する指標となります。
誤解を恐れずに言えば、適切に相関係数を算出するために、部分相関係数や偏相関係数などを用いることが多いので、個人的には、ここで挙げた選択肢群はひとまとまりというイメージで捉えています。
以上より、選択肢③、選択肢①および選択肢④は「2×2のクロス集計表における2変数間の関連性を示す指標」として不適切と判断できます。
⑤ 四分点相関係数
研究の内容によっては、得られるデータがいくつかのカテゴリー(男性/女性や賛成/中立/反対など)に分類されるようなカテゴリカルな変数の場合があります。
2つ以上のカテゴリカルな変数の間の関連について検討する場合には、それらの変数を組み合わせて度数分布表を作成する必要があります。
このような分析を「クロス集計」といい、クロス集計によって作成される度数分布表を「クロス集計表」または「分割表」と呼びます。
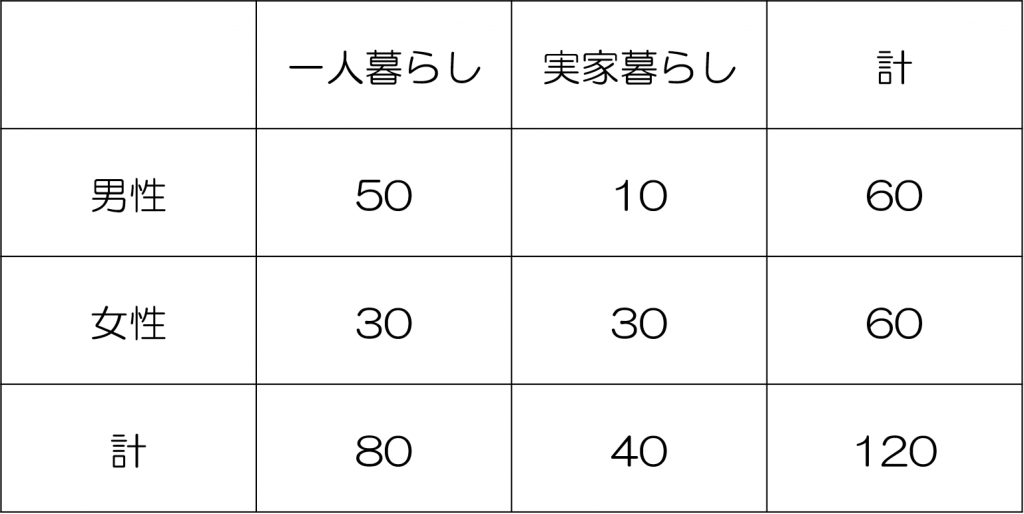
こちらのような、多くの人が見たことがあるであろう表がクロス集計表になります。
そして、このクロス集計表を用いて、2つのカテゴリカルな変数の間の関連の強さ(およびその方向)を表す測度のことを「連関係数」と呼びます(要は、この表を一つの値に集約する指標のことです)。
連関係数の中には、2×2のクロス集計表にのみ適用されるものと、k×l(いずれも2以上の任意の整数)のクロス集計表全般に適用できるものとがありますが、本問でテーマになっている2×2のクロス集計表に適用できる連関係数は「四分点相関係数(φ:ファイ)」や「ユールの連関係数(Q)」になります(四分点相関係数=φ係数とも言います)。
なお、このカテゴリカルな変数は、名義尺度(順序関係を持たない性別や血液型などのようなもの)によるものと、順序尺度(カテゴリーの順序に意味を持っている。徒競走の順番のようなもの)によるものに分けられます。
各変数が完全に名義尺度であるか、順序性がある変数(順序尺度)であるかによって、適用される連関係数は異なってきますし、順序尺度が入ってきている場合は四分点相関係数は適用することができません。
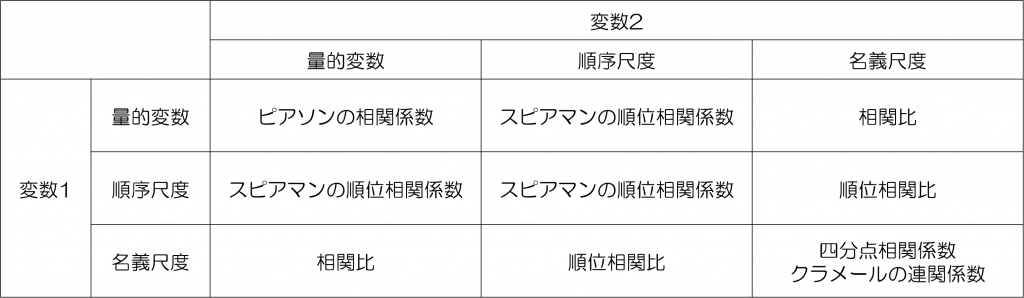
こうして表にしてみるとわかりやすいかもしれないですね。
なお、「φ(ファイ)係数」「クラメールの連関係数」などを算出するにあたっては、「χ2検定」を行います(この辺が「公認心理師 2018追加-82」を解くうえでは求められていた)。
このように、四分点相関係数は「2×2のクロス集計表」にのみ適用することができ(他に2×2に適用できるのはユールの連関係数があります。クラメールの連関係数はそれ以上でもOK)、2変数間の関連性を示す指標と言えます。
よって、選択肢⑤が適切と判断できます。
② 順位相関係数
すでに述べた通り、変数の種類が順序尺度の場合は、順位相関係数が用いられることになりますが、これを含めて順位相関係数が用いられる状況は以下のようにまとめることができます。
- 各データが、最初から順位で表されているような場合。
- データが得点で表されていたとしても、その得点(変数)が間隔尺度としての条件を満たしているとは考えられない場合(単位が常に一定ではないものなど)。
- 外れ値が存在し、ピアソンの積率相関係数ではその影響を大きく受けてしまう場合。
- 分布が極端に正規分布から離脱しており、有意性の検定における前提条件という点からピアソンの積率相関係数の適用が妥当ではない場合。
- 2変数間に特定の関数関係が想定せず、単調増加(単調減少)関係のみを問題にする場合。
これらの中で、おそらく試験に出るのは1だけだろうと思っています(そこまで複雑なものを出すのはあまりにも過酷)。
さて、順位相関係数は、同じ項目のセットに関する異なる順位同士の関係を検討します。
2種類の順位の一致を測定し、その統計的有意性を評価するものであり、代表的なのが「スピアマンの順位相関係数」と「ケンドールの順位相関係数」です。
他選択肢の解説において、すでに順位相関係数が本問の解答としては不適切なことは示してありますから、ここでは順位相関係数の基本的な考え方を具体例を示しながら説明しようと思います。
近年、ミス〇〇とかミスター〇〇のコンテストは、さまざまな社会情勢の中で控える傾向にありますが、それを強行して行ったとします。
Aさん(君)、Bさん(君)、Cさん(君)の3名がエントリーし、審査員であるO杉とP子がそれぞれ1位~3位の順位をつけていったとしましょう。
この場合、以下のような6パターンが考えられますね。
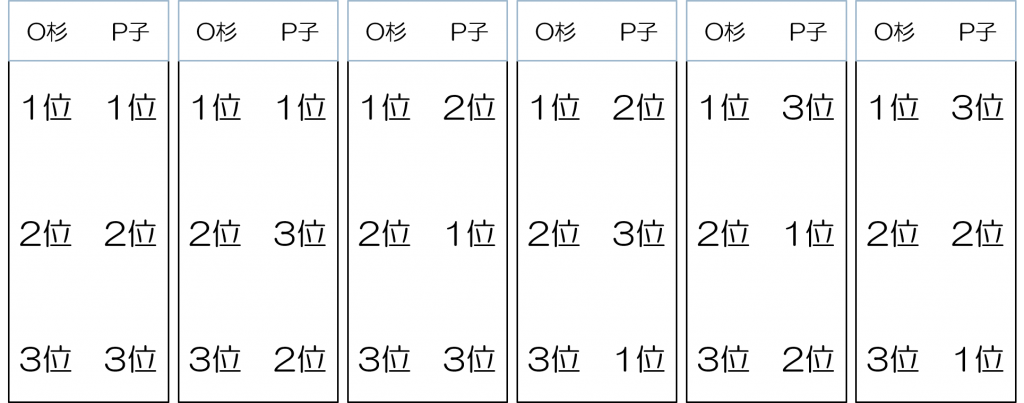
このように完全に一致(一番左)する場合から、完全に不一致(一番右)となる場合までが考えられるわけです。
ここで大切なのは、各順位同士を掛け合わせて合計を出してみることです。
すると、完全に一致している場合は14((1×1)+(2×2)+(3×3)の合計)になり、完全に不一致な場合は10((1×3)+(2×2)+(3×1)の合計)となります。
つまり「その順位同士を掛け合わせると、完全に一致しているときに最大の値を示し、完全に不一致のときに最小の値を示す」ということが言えます。
この性質を利用し、1を示すときには完全に一致、-1を示すときには完全に不一致になるような指標をスピアマンは作ったわけで、これが「スピアマンの順位相関係数」になります。

これがスピアマン。ちなみにピアソンの弟子。
非常に単純化して説明しましたが、以上が順位相関係数の基本的な理解になります。
以上より、選択肢②は「2×2のクロス集計表における2変数間の関連性を示す指標」として不適切と判断できます