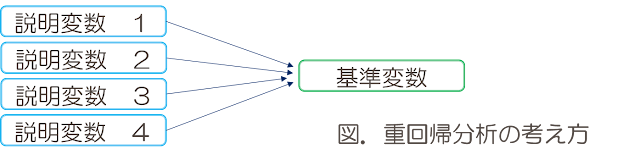
重回帰分析で算出される重相関係数の説明を選ぶ設問です。
何となく覚えているだけだと間違えてしまいそうな問題になっています。
普段から重回帰分析に馴染みのある人にとってはボーナス問題だったかもしれないですね。
(私にとってはそうではありませんでしたが)
解答のポイント
重回帰分析の基礎的な理解があること。
重相関係数について理解していること。
説明変数、基準変数などの用語の意味を理解していること。
基本的用語
- 独立変数:
実験研究領域において研究者が操作する変数を指して「実験変数」や「処理」と呼ぶが、「従属変数」との対比で「独立変数」と呼ぶのが一般的です。
調査研究領域では「独立変数」のことを、「説明変数」とも呼びます。 - 従属変数:
実験研究領域において「独立変数」に依存して変化する変数のことを「従属変数」と呼びます。
調査研究領域では「従属変数」のことを、「目的変数」「基準変数」とも呼びます。
重回帰分析とは
独立変数も従属変数も量的データであり、「すべての変数の間で相関係数を算出できるとき」の分析には、「重回帰分析」を用いることができます。
重回帰分析を使用できるのは、複数の独立変数によって1つの従属変数を説明しようというモデルにおいてです。
この時、独立変数相互の相関関係にも考慮し、その影響を取り除いて、各独立変数の純粋な影響を取り出すのが狙いとなります。
イメージとしては以下の通りです。
重相関係数とは
重回帰分析で重要なのは「標準偏回帰係数」と「重相関係数」です。
- 標準偏回帰係数:
他の変数の影響を取り除いた時の、説明変数の影響の大きさと向きを表します(βであらわされる)。
つまり、説明変数が基準変数に与える重みのことを指します。他の説明変数の影響を除き、当該説明変数のみで基準変数にどの程度重みをもつかを見ます。 - 重相関係数:
説明変数全体での影響の大きさを表します。よって重相関係数は1つのみです。
基準変数と予測値との相関係数を指します。
ただし、影響の向きを表すものではないので値は常に正の数になります
一般にRで表され、普通の相関係数(r)は区別のために「単純相関係数」や「単相関係数」と呼ばれます。
選択肢の解説
『①説明変数間の相関係数のことである』
この点は「多重共線性」について理解していることが求められます。
重回帰分析は、説明変数同士の相関が高い場合は行うことができません。
説明変数(例えば「胸囲」「腹囲」とします)の中に、相関係数が高い組み合わせがあると、もし腹囲と胸囲の相関係数が極めて高かったら、説明変数として両方を使う必要がなく、連立方程式を解くのに式が足りないというような事態になってしまうのです。
連立方程式は変数と同じ数だけ独立した式がないと解けないということを中学生の時に習ったと思いますが、同じような現象です。
説明変数間の相関がとても高い場合、回帰モデルは非常に不安定になり、説明変数の間にすでに別の線形回帰関係が含まれているということを指します。
その意味でこのような現象を「多重共線性」と呼びます。
一般に説明変数間の相関が0.7あれば、重回帰分析を控えます。
よって、選択肢①の内容は「多重共線性」と関連したものであり、重相関係数の説明としては誤りと言えます。
『②基準変数と予測値との相関係数のことである』
具体例を示しながら考えた方がわかりやすいように思えます。
説明変数を「労働時間」「神経質度合」として、基準変数を「ストレス」とします。
重回帰分析では、「労働時間」「神経質度合」を重回帰式に放り込んで計算した予測値(理論値;推定値)が存在します。
これはあくまでも推定値なので、理論的に示されたものにすぎません。
設定した「労働時間」「神経質度合」などの説明変数の精度が高いほどに、「ストレス」という基準変数を説明する力が強くなります。
一般に説明変数の精度が低いと、他の要因が絡んできて誤差が大きくなるため、予測値(理論値、推定値)から大きくずれていってしまいます。
つまり、予測値と基準変数の相関が高いということは、そこで設定された説明変数によって基準変数を説明する力が強いと言えるのです。
そこで、この予測値と、実際に示された「ストレス」の数値(=基準変数、実測値)の相関を「重相関係数」と呼び、これを算出することでその重回帰分析で研究者が設定した説明変数の価値が見えてきます。
以上より、選択肢②の内容は正しいと言えます。
『③説明変数と予測値との相関係数のことである』
こちらは上記の説明とは全く異なる内容となっています。
よって選択肢③は誤りと判断できます。
『④説明変数と基準変数との相関係数のことである』
意外とこちらと勘違いしてしまう人がいるかもしれません。
(上記の図だけを見ると、これかもと思ってしまうような気もします)
「重相関係数」の順番は以下の通りです。
- 示された説明変数より、予測値(理論値)を設定する。
- 予測値と示された基準変数(実測値)の相関を見る。
- 相関が高いと、説明変数で基準変数を説明できる面が大きいと判断できる。