因子分析の斜交回転において各観測変数と各因子との相関係数を要素とする行列を表すものとして、正しいものを1つ選ぶ問題です。
色んな本を読みましたが、どうしても専門用語が多くなり分かりづらい解説になってしまいます。
できるだけ平易に書いていこうと思います。
解答のポイント
因子分析の概要を把握していること。
直交回転と斜交回転の行列の違いを把握していること。
因子分析の概説
【因子分析とは】
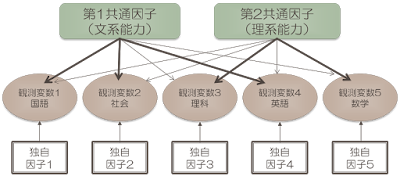
因子分析は、様々な変数間にある共通因子を抽出する方法です。
言い換えれば、「きっと世の中に存在するに違いない「データの背後に潜む説明変数(独立変数)」を見つけ出す」分析手法です(下の図を参照にして下さい)。
見つけ出すと言っても、各共通因子には固有の意味はありません。
分析後に分析者が「後知恵」で「主観的」に解釈するのです。
国語だったら普段の読書量とかですね。
その部分に影響を与える潜在的な変数も想定し、それは対応する観測変数だけに影響を与える(読書量は国語にだけ影響を与える)ので、「独自因子」と呼びます。
つまり、因子分析とは、独自因子を想定した上で共通因子を発見しようとする手法と言えます。
【因子分析の手順】
因子分析の手順は以下のようなものです。
放送大学から出ている「心理・教育統計法特論」を参照にしつつ述べていきます。
第1段階から順を追って説明していきます。
第1段階:観測変数の指定
まずは分析の対象になる観測変数を指定します。
観測変数は原則として間隔尺度か比例尺度になります。
例で言えば、5教科の点数などですね。
第2段階:初期解の計算
因子軸の回転を行う前に、とりあえずの結果(初期解)を出しておくことが必要になります。
そのために、ここでは因子の抽出方法(因子負荷量を推定する方法)を選択肢、因子数やその決定の仕方を決めておきます。
大切なのは、研究内容等を勘案して決めることです。
「この方法で良い結果が出なかったから、こっちの方法でやろう」というのは研究者として不適切な態度と言えます。
研究内容を勘案すれば、一番適した方法が自ずと見えてくるはずですから。
第3段階:因子軸の回転
初期解で複数の因子が抽出される(例で言えば、第1共通因子と第2共通因子が出てきた状態)と、多くの場合、そのままでは因子の特徴が明確に把握できません。
そこで因子パターンを単純構造に近づけるために、つまりは因子の解釈をしやすくするために、因子軸の回転を行います。
ここで言う単純構造とは「それぞれの項目の因子負荷が特定の因子だけに大きく、残りの因子に対しては非常に小さいような構造」を指します。
つまり「この項目はあの因子だけに負荷がある、あっちの項目はこっちの因子だけに負荷がある」といった状態です。
仮に以下の図のように6つの観測変数から2つの因子が抽出されて因子負荷量(影響の度合い)を座標空間にプロットしたとき(図の左側)、この座標軸(因子軸)を原点を中心に回転させてみます(図の右側)。
上記は因子軸を直角に保ったまま回転させているので、それぞれの点の原点からの距離や、点とテントの位置関係は変わっていません。
しかし、因子軸が点の集まりに近づくことによって、点は一方の因子と高い関連を持ち、因子負荷量(影響の度合い)が大きくなります。
同時に他方の因子との関連は低くなり、因子負荷量(影響の度合い)が小さくなります。
つまり、因子軸の回転によって、因子パターンが単純構造に近づき、因子負荷量にメリハリがつき、因子の特徴がわかりやすくなったといえます。
単純に言えば、より「文系能力」「理系能力」と言いやすくなったわけです。
因子軸の回転方法は、上記の直交回転と斜交回転に大別されます。
直交回転は、因子同士が無相関であるという前提で、因子軸が直角に交わったまま回転させる方法です。
斜交回転は、因子間の相関を認め、因子軸をそれぞれ別々に回転させる方法です。
斜交回転の例は以下の通りです。
ちなみに直交回転の代表的方法が「バリマックス回転」であり、斜交回転の代表的方法が「プロマックス回転」です。
第4段階:因子の解釈
因子パターン全体に目を配りながら、各因子に高い負荷量を示した観測変数のまとまりに着目し、そのまとまりに適した名称をつけます。
この際、他の因子と明確に区別がつくような名称をつけることが大切です。
ただし、因子間に相関を認めた斜交回転を行った場合には、因子間の関連の大きさを考慮に入れた名称をつける必要があります。
それぞれの因子に妥当な解釈ができない場合には、前のいずれかの段階に戻って再分析を行います。
第5段階:因子得点・尺度得点の計算
因子得点は、因子ごとに各観測変数の重みづけを考慮した得点です。
因子得点を用いると、個々の研究対象がそれぞれの因子の特徴をどのくらい持っているかを調べたり、個人をグルーピングしたり、他の変数との関連を検討したりします。
尺度得点とは、因子ごとに高い負荷を示した観測変数の値を単純に合計したものです。
尺度得点は因子得点の推定値とみなされ、さまざまな分析に使用されます。
以上が因子分析の大まかな流れになります。
こうした全体の流れを踏まえて、選択肢の検証に入っていきます。
選択肢の解説
『①共通性』
因子分析モデルでは、各観測変数は潜在変数である「共通因子」と、各観測変数に固有の「独自因子」の和で表されます。
このときの観測変数の分散(バラつき具合)は、「共通因子の分散」と「独自因子の分散」の和になります。
「共通性」とは、共通因子に基づく分散を各変量の分散で除した値であり、共通因子の変動の各観測変数の変動における割合になります。
難しく述べてありますが、平たく言えば「共通性とは、各観測変数に対して共通因子の部分がどの程度あるのかを示す指標」です。
数字は0~1であらわされ、その観測変数の全てを共通因子で説明できれば「1」になります。
以上より、選択肢①は誤りと判断できます。
『②独自性』
各観測変数に独自に備わっている変数のことを「独自因子」と呼びます。
例えば、国語と英語に共通している因子があるとして(これを例えば「文系能力」とするなど。これが「共通因子」です)、国語なら国語、英語なら英語にのみ働く因子も存在します。
例えば、国語なら読書量が多いか少ないか、英語ならアメリカ人の彼女がいるかいないかなど。
独自性とは、独自因子の分散(バラつき具合)を、対応する観測変量の分散で除した値です。
独自因子は「観測変数に固有な因子」と「誤差」に分解して考えることができ、その場合には独自性は両者の分散の割合の合計となります。
平たく言えば、「共通性とは逆に、共通因子で説明できない部分のこと」を独自性と呼びます。
共通性は、観測変数を説明する力が大きいほどに「1」に近づきますから、独自性は「1-共通性」で表すことができます。
「共通性+独自性=1」ということですね(1はすべてを説明できますよ、ということ)。
以上より、選択肢②は誤りと判断できます。
『④因子負荷』
上記でも述べたように、直交回転は「因子同士が無相関であるという前提で、因子軸が直角に交わったまま回転させる方法」、斜交回転は「因子間の相関を認め、因子軸をそれぞれ別々に回転させる方法」です。
この点により、表示される行列が両者で違います。
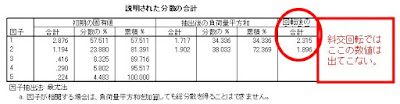
直交回転の場合は、因子同士が無相関であるという前提ですから、出てくるのは「因子負荷量」のみになります。
わかりやすい図があったので貼っておきます。
上記のように「回転後の因子負荷量」は直交回転なら記載されますが、斜交回転だと表示されないということになります。
選択肢の「因子負荷」は「因子負荷行列」のことを指しており、これは直交回転の行列を現わすものとなります。
問題は「斜交回転において」という記載がありますから、こちらの選択肢は誤りと判断できますね。
よって、選択肢④は誤りと判断できます。
『③因子構造』
斜交回転をした場合に因子負荷行列らしきものがいくつか出てきます。
斜交回転ででてくる行列は「因子パタン行列」「因子構造行列」「基準構造行列」の3つです。
- 因子パタン行列:直交回転における因子負荷に該当する。「回転後の負荷量平方和」欄に「合計」しか出力されない。
- 因子構造行列:因子と変数の相関係数。単に「構造行列」とも呼ぶ。
- 基準構造行列:他の因子の影響を取り除いた場合の因子の変数における負荷。
斜交回転は「因子間の相関を認め、因子軸をそれぞれ別々に回転させる方法」ですから、上記のような因子構造行列が示されるということになります。
直交回転では相関を前提としていませんので、因子構造行列が示されることはありません。
因子構造行列は以下のような形になります。
これが因子と変数の相関を示したものになります。
まとめると、以下の通りになります。
- 斜交回転では、因子間の相関を前提としている。
- そのため、斜交回転によって結果を(SPSSとかで)算出すると、直交回転よりも多くの行列が結果として示される。
- そのうちの一つである「因子構造行列」は、因子と変数の相関係数を示していて斜交回転を行ったことによって示されたということになる。
すなわち選択肢にある「因子構造」は、この「因子構造行列」を指していると考えられます。
よって、選択肢③が正しいと判断できます。
『⑤単純構造』
単純構造を得るのは、因子回転による場合が多いです。
単純構造とは「それぞれの項目の因子負荷が特定の因子だけに大きく、残りの因子に対しては非常に小さいような構造」を指します。
つまり「この項目はあの因子だけに負荷がある、あっちの項目はこっちの因子だけに負荷がある」といった状態です。
因子軸の回転を行うことによって、単純構造に近づけていくということを上記で示しました。
単純構造に近づけることの目的は、解釈しやすくするためです。
因子分析において「解釈しやすくする」ということは、因子に名前を付けやすくなるということになります。
よって、選択肢⑤は誤りと判断できます。