測定値の分散に対する真値の分散の割合で定義される値を選択する問題です。
あまりに種類が多いものもあり、「これはこういう計算式ですよ」と一概に言えないことが多い問題でしたね。
問83 測定値の分散に対する真値の分散の割合で定義される値として、正しいものを1つ選べ。
① 相関係数
② 変動係数
③ 連関係数
④ 信頼性係数
⑤ 妥当性係数
選択肢の解説
① 相関係数
そもそも「相関」とは、2つの変数がどのくらい一緒に変動するかを示す概念であり、2変数の直線相関が最も一般的(ピアソン)で、この場合、2変数の関係は直線であらわすことができます(一般的に「相関係数」といえば、ピアソンの積率相関係数を指すことが多いです)。

こちらがピアソン(名は元Carlであったが、のちにカール・マルクスに傾倒して自らKarlと変えた)。
「2変数の直線相関」というのも少しわかりにくい表現かもしれませんが、実態はそれほど難しい話ではありません。
要は「片方が上がる(下がる)とき、もう片方はどうなるの?」ということであり、身長と体重で言えば「身長が上がれば、体重も上がる傾向にある」という片方が上がればもう片方も上がることを正の相関と呼び、気温とおでんの売り上げで言えば「気温が上がれば、おでんの売り上げは下がる」という片方が上がればもう片方が下がることを負の相関と呼ぶのです。
以下のように座標軸でプロットされることになりますね。
こうしたx軸とy軸を作り、各ケースのデータをプロットして、両変数間の関係を表したものを一般に「散布図」と呼び、相関係数を用いるときに使う図表と理解しておいてください。
相関係数では、直線的な関係(比例関係)の強さを、1 から-1 の間の数で表し、相関係数の絶対値が1に近いほど、相関関係が強くなります。
相関係数の意味や使い方を理解したところで、ここでは公式と導出するステップを見ていきましょう。
xとyの間の相関係数(r)は、以下の公式で求まります。
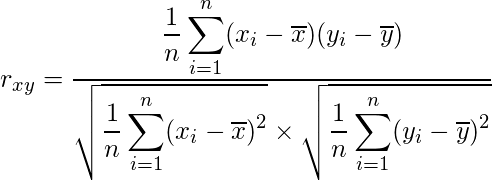
ちなみに、n(データ(xとy)の個数)、xiおよびyi(xyそれぞれの個々の数値)、x(xの平均)、y(yの平均)になります。
上記だけを見てもちんぷんかんぷんだと思います。
そういう人のために、資料室に「公認心理師 勉強会資料」があり、この中に「統計・研究法(⑤心理学における研究・⑥心理学に関する実験)」があります。
この資料の中で、相関係数の式がこうなっているのかについて説明してあります。
上記の計算式を見れば、少なくとも相関係数が、本問で示されている「測定値の分散に対する真値の分散の割合で定義される値」で説明できるほど単純なものではないことはわかると思います。
よって、選択肢①は誤りと判断できます。
② 変動係数
変動係数(Coefficient of Variation)は、標準偏差を平均値で割った値のことで、単位の異なるデータのばらつきや、平均値に対するデータとばらつきの関係を相対的に評価する際に用いる単位を持たない(=無次元の)数値です。
こちらのサイトに例題が載っていたので、こちらを参考にしておきましょう。
次の表は、あるスーパーマーケットで肉の値段を10日間調査した結果をまとめたものです。この調査の結果、鶏ささみは100gあたり平均80円、標準偏差は20円でした。一方、牛ステーキ肉は100gあたり平均1800円、標準偏差は300円でした。どちらの肉の方が値段のばらつきが大きいでしょうか。
| 肉の種類 | 平均価格(円) | 標準偏差(円) |
| 鶏ささみ肉 | 80 | 20 |
| 牛ステーキ肉 | 1800 | 300 |
標準偏差の値をそのまま比較すると牛ステーキ肉のばらつきが大きいことが分かります。これは、牛ステーキ肉の値段が高いため、鶏ささみと比較して標準偏差の値が大きくなってしまっているためです。
このような場合に変動係数を用いると、それぞれの平均値に対する相対的なばらつきの大きさを見ることができます。
- 鶏ささみの変動係数:20÷80=0.25
- 牛ステーキ肉の変動係数:300÷1800≒0.167
変動係数を計算すると、平均値に対しては鶏ささみの値段の方が相対的にばらつきが大きいという結果になりました。
このように、変動係数とは「単位の異なるデータのばらつきや、平均値に対するデータとばらつきの関係を相対的に評価する際に用いる単位を持たない(=無次元の)数値」であり、その算出方法は「標準偏差を平均値で割る」になります。
よって、本問で求められている「測定値の分散に対する真値の分散の割合で定義される値」ではないことがわかりますね。
以上より、選択肢②は誤りと判断できます。
③ 連関係数
連関係数とは、クロス集計表における行要素と列要素の連関の度合いを表す係数のことであり、この連関の度合いを表す指標として「クラメールの連関係数V」「ピアソンの連関係数C」「チュプロウの連関係数T」「グッドマンとクラスカルの予測連関係数λ(ラムダ)ならびに順序連関係数γ(ガンマ)」があります。
要は「2つの質的な順序変数間の連関の大きさを表す指標」であると考えておきましょう(ちなみに、γ係数は -1から1の値を取る。0が連関無し、1が完全な正の連関、-1が完全な負の連関を意味する)。
なお、グッドマンクラスカルのγ係数は同順位のペアをうまく扱えないという特徴があるので、それを踏まえて活用する必要があります。
また、連関係数の中には、2×2のクロス集計表にのみ適用されるものと、k×l(いずれも2以上の任意の整数)のクロス集計表全般に適用できるものとがありますが、2×2のクロス集計表に適用できる連関係数は「四分点相関係数(φ:ファイ)」や「ユールの連関係数(Q)」になります(四分点相関係数=φ係数とも言います)。
φ係数もクロス集計表における行要素と列要素の関連の強さを示す指標であると言えます。
なお、φ係数は集計表の行列のサイズにより上限が異なるので、行列が等しい集計表の間でしか比較する意味が出ないという特徴があります。
連関係数の求め方についてですが、上記にもあるように様々な指標があります。
全部書くと煩雑になるので、クラメールの連関係数についてのみ算出方法を述べておきます。
まず、クラメールの連関係数とは「カテゴリデータ同士の相関係数」だと思っておけばOKです。
クラメールの連関係数では、まず期待度数(行要素の合計や列要素の合計の比率から逆算して期待される度数のこと)を求めます。

そして、上記がクラメールの連関係数の算出方法になります。
よくわからない人も多いと思いますが、本問においては「測定値の分散に対する真値の分散の割合で定義される値」ではないことがわかればOKです。
以上より、選択肢③は誤りと判断できます。
④ 信頼性係数
信頼性とは、尺度の精度を指す用語であり、要するに「何回やっても同じ結果が得られるか」ということを示した指標になります。
信頼性の程度を示すものとして「信頼性係数」があり、これは「「真の値の分散」÷「測定値の分散」として計算されます。
つまり「全体の得点の分散に占める真値の分散の割合」を意味しており、これは本問で提示されている「測定値の分散に対する真値の分散の割合で定義される値」と合致するものですね。
上記だけではよくわからない人もいると思いますのでもう少し詳しく言うと、誤差とは「データのばらつきを表したもの。平均値からの距離」だと思ってください。
また、真値とは「被験者の英語の実力」みたいなものであり、存在はするけど本当の意味で測定することが困難なものになります(ですから、真値は本質として不明なものです)。
これに合わせると、誤差は「被験者の体調、天気」などになりますね。
信頼性は、再現性・等価性・内的整合性という3つの概念で測定されることが多いので、それを少し詳しく述べていきましょう。
まずは各概念を簡単に説明すると以下の通りです。
- 再現性(安定性):
検査結果の再現性が高く、同一の検査対象であるなら何度測定を繰り返しても同じような測定値が得られるほど、安定しており信頼性が高いとする概念のこと。 - 等価性:
検査が測ろうとしている構成概念と同じ、あるいは似通った概念を測る他検査と一定の関係が認められれば、信頼性が高いとする考え方の概念のこと。 - 内的整合性(内的一貫性):
検査の尺度内部で回答のバラツキがないことを意味する。
尺度内の各項目が構成概念を同じように測ることができて、バラツキがなく、一貫していることを信頼性が高いとする考え方の概念のこと。
イメージしにくいのは内的整合性かなと思いますが、こちらは外の基準と比べたりするのではなく、その検査を構成している項目同士が同じような力を持っているかを見るものです。
不安検査で、ある項目が不安を検出する力が5くらいあっても、別の項目が2しかないと項目間のバラつきが大きいと判断されるわけですね。
さて、この3つはあくまでも信頼性を見るための「概念」にすぎません。
この各概念に沿って、実際に信頼性を測定する「方法」が必要になります。
その「方法」によって検出されるのが「信頼性係数」となります。
「概念」と「方法」の組み合わせについては以下の通りです。

右側にあるのが各概念に沿った代表的方法となりますね。以下では各推定法を簡単に述べていくことにしましょう。
- 再検査法:
再現性(安定性)によって信頼性を推定する方法。一定期間(2週間から1ヶ月)をおいて、同じ検査を行い、その二つの得点間の相関係数を信頼性係数とする。 - 平行検査法(代理検査法):
等価性によって信頼性を推定する方法。測定したい検査と、項目数・質問内容の難易度・測定したい構成概念・分布・平均値・分散などがほぼ等しい検査を作成もしくは使用して、その二つの検査間の相関係数を信頼性係数とする。 - 折半法:
内的整合性(内的一貫性)によって信頼性を推定する方法。同一の対象に2回検査を実施することが困難な場合もある。そこで、例えば、ある検査を偶数項目と奇数項目に折半し(奇遇法)、二つの尺度とみなしてその相関係数を信頼性係数とする。このやり方を「スピアマン・ブラウンの公式」と呼ぶ。 - クロンバックのα係数:
内的整合性(内的一貫性)によって信頼性を推定する方法。例えるなら項目群の可能なすべての組み合わせについて相関係数を算出して平均を求めたような感じ。そのため、折半法をより一般化した推定方法と言える。α係数は0~1の値を取り、1に近づくほど信頼性が高い。ただし、このやり方だと、項目の中に似通ったものがあるほど、信頼性係数は高くなってしまう。項目数を増やすほどに信頼性は高くなってしまう。 - キューダー=リチャードソンの公式:
内的整合性(内的一貫性)によって信頼性を推定する方法。2値的採点(例えば、正答を1に、誤答を0)の項目のみから構成されるテストに適用できる。 - 項目分析:
内的整合性(内的一貫性)によって信頼性を推定する方法。検査作成時に、予備調査によって得られたデータから各項目の等質性や鑑別力を検討し、適切でない項目を除外したり、表現や内容の一部を修正したりすることで検査を精錬してゆく重要な手続きであり、必要に応じて予備テスト→項目分析のプロセスを数回繰り返すこともある。 - コーエンのκ(カッパ)係数:
再現性(安定性)によって信頼性を推定する方法。2回の調査の安定性や、偶然の一致を考慮した二人の評定者間の評定の一致度を表す。すなわち「偶然の一致率(Pc)を考慮した一致率の算出法」となる。X(一致率)=(P0-Pc)/(1-Pc)。
それぞれのやり方について簡単な計算方法を述べましたが、これをまとめて説明すると「測定値の分散に対する真値の分散の割合で定義される値」になるということです。
上記の通り、本問の「測定値の分散に対する真値の分散の割合で定義される値」については信頼性係数のものであると言えますね。
よって、選択肢④が正しいと判断できます。
⑤ 妥当性係数
信頼性係数と似たような概念として、妥当性係数がありますね。
妥当性とは尺度が「測りたいものを測定しているかどうか」を意味する概念であり、その種類は様々なものがあります。
それ故に、計算方法も一概に言えないので、信頼性係数と違って「妥当性係数はこうやって求める」とまとめて述べることができません(一般には相関係数で表すわけですが、そうではないものも多いのでまとめられない)。
以下では、その種類ごとの特徴について述べていくので、算出法を一概に述べることの難しさを感じてもらえればと思います。
妥当性にはいくつか種類があり、代表的なのは構成概念妥当性・内容的妥当性・基準関連妥当性になりますから、まずはこれらについて詳しく述べていきましょう。
まず構成概念妥当性・内容的妥当性・基準関連妥当性は以下のようなものです。
- 構成概念妥当性:
測定しようとしている構成概念または心理学諸特性を検査でどのくらい測定できているかを問う概念。 - 内容的妥当性:
あるテストや検査の項目が、測定しようとする内容領域に適切であるかどうかの程度。専門家が理論的に判断する。 - 基準関連妥当性:
測定したものが、それとは別の外的基準とどの程度関連があるかによって判断されるもの。
そして、これらはまた細かく分類されていきます。
構成概念妥当性に含まれるものは以下になります。
- 収束的妥当性:
理論的に同じ構成概念を測定していると考えられる別の検査との相関で示される妥当性。
相関係数が高いほど妥当性が高い。 - 弁別的妥当性:
別の構成概念を測定していると考えられる検査との相関で示される妥当性。
相関が低いほど妥当性が高い。 - 因子妥当性:
データの因子分析を行い、下位尺度が予測通りの因子に分かれるかどうかを検討することで示される妥当性。
弁別的妥当性については、例えば、「うつ病」と「非うつ病のうつ状態」を見分ける場合などに大切になってきますね。
MMPIなどは「うつ病」ではなく「うつ状態」を検出するとされていますが(もちろん、うつ病も検出されることになる)、これらを分けて検出できるようにしたい場合は弁別的妥当性が重要になってくるわけです。

こんな感じのイメージですね。
内容的妥当性に分類されるもの
- 表面的妥当性:
検査が被験者にとって妥当であるか、または何を測定しているように見えるかを表す概念。これが低いと被験者のテストに対する動機づけを損なう可能性がある。
テスター、テスティの両方が判断する。 - 論理的妥当性:
測定される領域があらかじめ明確に決められているときに、テストの質問項目や課題内容がその領域を十分に代表しているか否かを示し、専門家によって判断される妥当性。
表面的妥当性はちょっと馴染みづらい考え方かもしれません。一般に心理検査では、結果に歪みが生じないように「受験者が何を測っているか分からない」ことが重視されることも多いですから。ですけど、例えば就職適性を測る検査の場合などでは「こんな質問で何を測ってるんだよ?」と思われると、曖昧に答えてしまうなどの反応が出てきてしまいかねませんよね。このように、検査によっては表面的妥当性が重視されることもあるということです。

こんな感じのイメージですね。
基準関連妥当性に分類されるのは以下になります。
- 併存的妥当性:
作成した検査と基準となる検査を同時に実施する場合を指す。
例えば、テストと面接を同時に行って、その評価の相関を見る等。 - 予測的妥当性:
作成された検査より後に基準となる検査を実施する場合を指す。将来の特性や行動が検査によってどれくらい予想可能かを表す(入試と入学後の成績、試験と売上、など)。
公認心理師試験が始まって、各社が「模擬試験」を作成していますね。
私は「模擬試験」であるならば、それがどの程度の予測妥当性を示したのかを公開すべきだと考えています(しているのかな?)。
つまり、模擬試験での点数が高かった人が、実際に公認心理師でも点数が高かったならば、その模擬試験は予測妥当性が高いと言えるわけですよね。
予測妥当性が高ければ、その模擬試験を来年度の受験生が受けることに大きな価値が見出されるわけです。
予測妥当性が高い模擬試験であれば点数が低くても、その内容を何度も勉強することで合格に近づいていると統計的に言えるわけですからね。
また、「模擬試験」と銘打つからには公認心理師の「模擬」であるはずなので、やはり妥当性を示すことでその名称に力を持たせることが求められると考えています(私が公開しているものを「確認テスト」という名称にしているのはそういうわけです。あくまでもブループリントの小項目にある知識を「確認」するためのものであり、実際に公認心理師試験を模したものではないということですね)。

このようなイメージになります。
上記以外の妥当性についてもいくつか挙げておきます。
- 内的妥当性:
研究から導き出された結果の正当性、因果類推(因果関係)の適切さを表す。 - 外的妥当性:
研究結果がどの程度他に適用できるかという一般化の可能性を表す。 - 交差妥当性:
ある標本で重回帰式などの予測式が成り立つとき、別の標本で同じ予測式が成り立つかどうかを確認すること。
例えば、アメリカで標準化された視覚検査が日本人に当てはまらない場合、交差妥当性が低いと言える。 - 差異妥当性:
瞳孔反射を測定することで、脳腫瘍がある人とない人を高い確率で識別できるとすれば一般にこの方法は差異妥当性が高いという。
特定の基準変数との相関は高いが、それ以外の基準変数とは相関が低いこと。
以上です。
上記からもわかる通り、妥当性の種類は豊富で、その切り口も様々です。
ですから、計算の仕方も、信頼性係数の「測定値の分散に対する真値の分散の割合で定義される値」のように一概に言えるものではありません(それぞれの切り口に応じて算出方法があるというイメージでいてもらえればいいかなと思っています)。
よって、選択肢⑤は誤りと判断できます