探索的因子分析において因子数を決定する基準に関する問題です。
正直なところ、ちんぷんかんぷんな選択肢もありましたね。
問5 探索的因子分析において、固有値の変化がなだらかになる1つ前までの固有値の数を因子数とする基準として、最も適切なものを1つ選べ。
① MAP基準
② V S S基準
③ カイザー基準
④ スクリー基準
⑤ ガットマン基準
解答のポイント
因子分析において因子数を決定する基準を把握している。
選択肢の解説
③ カイザー基準
⑤ ガットマン基準
ここではまず因子分析という統計手法が、どういう作業を行うものであるかを理解しておきましょう。
こちらについては「公認心理師 2020-81」を転記しますが、この内容は上記の書籍からの引用になります。
ある国の国民性に関するイメージについて調査を行う際、アンケート項目は以下のように設定されたとします。
- 時間を守りそうか
- メールをすぐに返しそうか
- 整理整頓が好きそうか
- 笑顔が多そうか
- 自分の意思を正確に伝えることが得意か
- 相手の意図を正確に汲み取るのがうまいか
これらの項目は独立しているが、1~3については「几帳面さ」、4~6については「コミュニケーション能力」についても尋ねているように見えるのはわかりますね。
このように、各項目は我々が持つイメージについて独立に問うものではありますが、背景には共通する評価軸が存在している可能性も考えられるはずです。
このように観測された変数(ここではアンケートの質問項目に対する評価点)に影響を与えているとされる、目に見えない要因(ここでは「几帳面さ」および「コミュニケーション能力」のような評価軸)で説明する統計的手法を「因子分析」といいます。
因子分析については「公認心理師 2018追加-6」において、「きっと世の中に存在するに違いない「データの背後に潜む説明変数(独立変数)」を見つけ出す分析手法」と説明していますが、これは上記の説明の言い方を変えているだけで、同じことを言っているのがわかると思います。
さて、本問にある「探索的因子分析」という用語についても確認しておきましょう。
因子分析は大きく分けて「探索的因子分析」と「確証的(確認的)因子分析」があります。
探索的因子分析とは「観測変数を規定する因子についての仮説を設定せず、因子を探索的に検討するための因子分析」になり、これに対して、確証的因子分析とは「因子について何らかの仮説があり、それが実際のデータにあてはめることができるかどうかを検討する因子分析」を指します。
確証的因子分析を用いるのは、ある尺度の因子がすでに探索的因子分析で抽出されていて、尺度のデータを改めて得たときに因子の仮説が妥当と言えるかを再度検証する場合などが考えられます。
とりあえず「探索的因子分析」と言われたときには、一般的に行われる因子分析を想定しておけば問題ないと言えるでしょう。
因子分析を用いた研究を行う場合には、研究者はパラメータ推定の方法だけでなく、因子数も決めておかなくてはなりません。
本問で問われているのは、この「因子数の決定の基準」の方法についてです。
一般に適正な因子数を選べなかった状況では、過小因子数のときに深刻なゆがみが生じることがあり、過大因子数の場合は1つまたは2つの顕著な負荷をもつ項目しかもたない因子が生じるとされています。
ですから、どういう基準で因子数を決定するかは、因子分析を行うにあたって重要項目と言えますね。
選択肢③のカイザー基準とは、相関行列の固有値1以上の数を因子数とするものを指します。
因子分析では観測変数の相関行列を扱い、相関行列に対して固有値という値が計算されます。
相関行列とは、「複数の変数間の相関係数を行列の形式でまとめたもの」であり、統計学の分野で広く使われます。
相関行列は、各変数のペア間の相関係数を表した正方形の行列で、対角線上には1が並び、相関係数は、2つの変数間の線形関係の強さを表し、-1から1までの値を取ることになります。
固有値とは、行列の固有ベクトルが線形変換後に何倍になるのかを示す値ですが、要するに「意味のある因子の数」だと思っておいてくれれば大丈夫です。
固有値は1つの相関行列に対して、通常観測変数と同じ数だけ計算されるので、例えば、10項目の質問紙データを因子分析する場合には固有値も10個計算されることになります。
これらの固有値のうち、1以上のものの数を因子数にしようというのが「カイザー基準」になります(ちなみに、このことをガットマンがカイザーよりも先に見つけたので「ガットマン‐カイザー基準」とも呼ばれます)。
カイザー基準は、因子間の相関が高いと因子数を過小に推測してしまうといった問題もあり、大雑把であまり当てにならないという研究結果も出ています(統計ソフトの初期設定になって使われることも多いのが、このカイザー基準です)。
以上のように、「相関行列の固有値1以上の数を因子数とするもの」がカイザー基準ですから、本問の説明とは合致しないことがわかりますね。
選択肢⑤の「ガットマン基準」と選択肢③の「カイザー基準」との違いが正直よくわからなかったので、まとめて記載してあります。
よって、選択肢③および選択肢⑤は不適切と判断できます。
④ スクリー基準
スクリー基準はCattellが提唱しました。
初期解の固有値を降順で並べた折れ線グラフが出力されます。
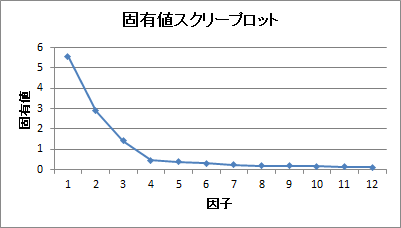
この折れ線で傾斜がゆるやかになっている部分のことをスクリーと言います。
そして、このスクリーが始まる前までの固有値の数を因子数とすることをスクリー基準と言います。
スクリー基準では、このグラフでなだらかになった場所(スクリー)を見て、固有値の減少がなだらかになる前までの因子数を採用することになります。
上記のプロットで言えば、スクリー(なだらか)の前までなので、3つの因子を因子数として採用することになるわけです。
以上のように、スクリー基準は本問の「固有値の変化がなだらかになる1つ前までの固有値の数を因子数とする基準」に合致することがわかります。
よって、選択肢④が適切と判断できます。
① MAP基準
② V S S基準
この2つに関しては、調べてもかなりわかりづらかったので、概要だけ述べて終わりにしておきます。
まず選択肢①の「MAP基準」ですが、MAP=Minimum Average Partial:最小偏相関平均です。
Velicerが開発した方法で、主成分を統制変数とする観測変数間の偏相関係数を求めます。
そして、その2乗平均を最小とする主成分の数を抽出因子数とする方法です。
「主成分を統制変数におき、観測変数間の偏相関係数を求めて、その2乗平均を最小にする主成分数を因子数にするもの」がMAP基準であると言えますが、正直かなりわかりづらいですね。
続いて、選択肢②の「VSS基準」ですが、よくわからなかったのが正直なところです。
こちらのサイトの「因子数の決定法のフロー」を見ると、スクリー基準、ガットマン基準、MAP基準などは因子数の推定で用いられますが、VSS基準は回転数などを決めた後の「さらに因子数を推定する」というところで記載されています。
どうもVSSは統計ソフトの関数に存在するようで(こちらのサイトなど)、統計ソフト以前世代の私にはちんぷんかんぷんでした。
いずれにせよ、MAP基準もVSS基準も本問の「固有値の変化がなだらかになる1つ前までの固有値の数を因子数とする基準」には合致しません。
よって、選択肢①および選択肢②は不適切と判断できます。