研究計画から最も適した分析方法を選択する問題です。
要因数、被験者間or内or混合、分散分析とt検定の違いなどの知識が問われています。
問82 観察者の有無が作業に及ぼす影響をみる実験において、参加者を作業時に観察者がいる群といない群に分け、各群の参加者に単純課題条件と複雑課題条件の双方を課した。
この結果の分析方法として、最も適切なものを1つ選べ。
① 2要因混合分散分析
② 2要因被験者間分散分析
③ 2要因被験者内分散分析
④ 複数個の1要因被験者間分散分析
⑤ 複数個の対応のある平均値のt検定
解答のポイント
分散分析、被験者間・内などの基本的な事項に関する理解がある。
選択肢の解説
① 2要因混合分散分析
② 2要因被験者間分散分析
③ 2要因被験者内分散分析
本問における「観察者の有無が作業に及ぼす影響をみる実験において、参加者を作業時に観察者がいる群といない群に分け、各群の参加者に単純課題条件と複雑課題条件の双方を課した」という研究デザインに最も合致する分析方法を考えていくことが重要になります。
まず、ここで挙げた選択肢を理解する上で大切なのは「被験者間・被験者内」の違いを理解しておくことです。
被験者内計画とは、同じ被験者が独立変数の異なった値をすべて体験することになります。
例えば、記憶実験で「暗記条件」と「イメージ条件」があるとしたら、両方で単語を記憶し、記憶テストを受けることになります。
同じ被験者を両方の条件に配分することになるので、2つの条件の間で被験者の記憶力に差はないことになります。
この実験によって記憶テストの成績に差が見られたとすれば、それは「記憶力のような個体差変数によるものではなく、暗記条件かイメージ条件かという独立変数によるものである」と確信をもって推定できるわけです。
しかし、残念ながら、多くの実験では、この理想的な被験者内計画を使うことができません。
被験者内計画の欠点として「残留効果に弱い」ということが挙げられます。
被験者内計画では同じ被験者が異なる条件を試行することになりますが、この際、前の試行から後の試行への影響が生じ、このことを「残留効果」と呼びます。
先の記憶実験でも、どちらかの条件を先に行うことで、後の条件の試行に影響を与えることを懸念せねばなりません(記憶実験の場合、試行順を変えたとしても、練習効果が生じる等の問題が大きい)。
このように、心理学の実験では、残留効果が否定できない場合が多いので、被験者内計画が使えない場合も多くなり、そうなると被験者間計画という「独立変数の値それぞれに、異なる被験者を割り当てる」という計画を選択することになります。
以上のように、被験者内計画は「同じ被験者が独立変数の異なった値をすべて体験する計画」であり、被験者間計画は「独立変数の値それぞれに、異なる被験者を割り当てる計画」ということになります。
これを踏まえて本問の「観察者の有無が作業に及ぼす影響をみる実験において、参加者を作業時に観察者がいる群といない群に分け、各群の参加者に単純課題条件と複雑課題条件の双方を課した」について考えてみましょう。
この計画において「参加者を作業時に観察者がいる群といない群に分け」というところは被験者間計画ですが、それに続く「各群の参加者に単純課題条件と複雑課題条件の双方を課した」というところは各群内に有されている2つの条件は同一の参加者が行う、すなわち被験者内計画であることがわかるはずです(イメージは以下の通り)。
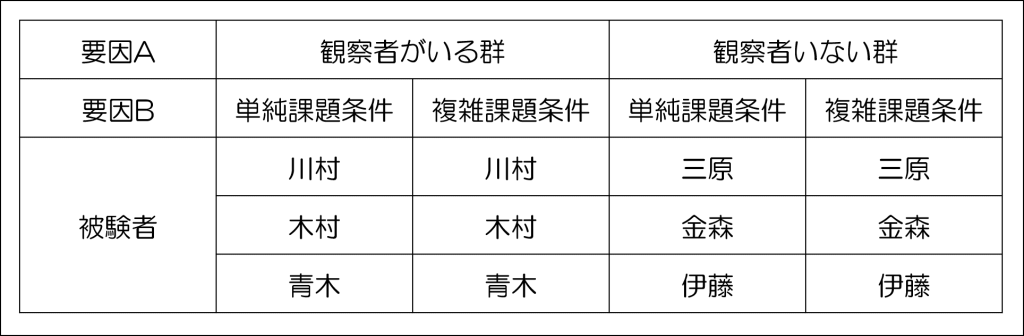
上記のように、2つの要因があって、要因Aではそれぞれ参加者が異なりますが、要因Bでは同一参加者が両方の条件を行うことがわかりますね(参加者の名前は適当です)。
こういう計画のことを「混合計画」と呼びますから、本問の計画は「混合計画」であると言えます(混合計画は本来、設定された要因を「被験者自身が備えている」という場合に用いられやすいです。例えば性別や年齢みたいな)。
また、上記の通り、本計画では2つの要因が設定されていますから「2要因」ということになります(この点は別選択肢の解説も参考にしてください)。
そして、本問の条件だとそれぞれの条件の成績によるバラつき(群間平方和)と自然に生じるバラつき(群内平方和)を比較する分散分析が行われることになります(平均値を活用するわけですから、従属変数が量的変数、独立変数が質的変数である必要があり、本問はその条件に合致しています)。
分散分析に関しては「公認心理師 2019-80」などに詳しく載せていますので、こちらも参考にしてください。
以上より、本問は分析方法としては2要因混合分散分析が最も適切と見なすことができます。
よって、選択肢①が適切と判断でき、選択肢②および選択肢③は不適切と判断できます。
④ 複数個の1要因被験者間分散分析
⑤ 複数個の対応のある平均値のt検定
既に解説の大半は終わっているのですが、これらの選択肢についてもう少し解説を加えていきましょう。
選択肢④の「複数個の1要因被験者間分散分析」では、例えば、本問の「観察者がいる群・観察者がいない群」という要因だけであれば1要因となりますね。
「複数個」ということで「単純課題条件・複雑課題条件」という要因もあるよ、ということを言いたいのかもしれませんが、当然それは間違いですね。
2要因の分散分析にすることで、2つの要因(2水準×2水準)での平均値に違いがあるかを知ることも本問では求められていますので、「複数個の1要因被験者間分散分析」ことはありません(そもそも「単純課題条件・複雑課題条件」に関しては被験者内計画ですしね)。
選択肢⑤については、t検定と分散分析の違いについて理解しておきましょう。
これらは両方とも平均値の比較を行う分析方法ですが、2群以内の平均値の比較であればt検定を、3群以上の平均値の比較であれば分散分析を用いると、とりあえずは単純に覚えておけば良いでしょう。
ですから、2要因(2水準×2水準)の本問の計画においてt検定を使うことはありません。
ちなみに「対応の有無」ですが、「対応のない要因」とは、その要因の異なる水準に含まれる従属変数の値が互いに独立である要因のことです。
たとえば、指導法の効果を比較する実験において「厳しい条件」「やさしい条件」にランダムに被験者を割り当てる場合、「指導法」という要因は対応のない要因であり、対応のない要因では、ある群の値から別の群の値を予想することができません。
対して「対応のある要因」とは、その要因の異なる水準に含まれる従属変数の値に相関がある要因のことです。
たとえば、指導法の実験において、マッチングによって各群に被験者を割り当てる場合や各群とも同一被験者で行う場合、「指導法」という要因は対応のある要因となります。
対応のある要因では、ある条件の測定値の高低によって、その被験者(ブロック)の別の条件における測定値がある程度予測できます。
まとめて言えば「対応のない要因の場合は、その要因の異なる水準に含まれる従属変数の値は互いに独立であるのに対し、対応のある要因の場合は、異なる水準に含まれる従属変数の値に相関がある」ということになります。
以上より、選択肢④および選択肢⑤は不適切と判断できます。