代表値についての問題です。
幾何平均、調和平均などこれまでの試験では出なかったものが出ていますね。
問5 観測値として、9、5、7、8、4が得られたとき、値が6.6となる代表値(小数点第2位を四捨五入)として、正しいものを1つ選べ。
① 中央値
② 幾何平均
③ 算術平均
④ 相乗平均
⑤ 調和平均
解答のポイント
各代表値の求め方、活用場面について理解している。
特に平均値の各種について使い分けを理解できていると良い。
選択肢の解説
① 中央値
まず問題文にある「代表値」という表現から理解しておきましょう。
代表値とは「データの中で最も一般的・典型的な値はいくつか」といった意味でのデータの特徴を端的に表す値です。
あるデータの、とある側面(分布)を要約するものと捉えても良いでしょう。
データの測定尺度によって異なりますが、さまざまな種類があります。
本選択肢の中央値は、よく使われる代表値の一つです。
Median(中央値:Me)は、データを大きさの順に並べたときに、ちょうど真ん中に位置する値です。
データが偶数の場合は、真ん中にある2つの数字の平均値(算術平均)を算出し、それを中央値とします。
本問の観測値は「9、5、7、8、4」ですから、これを大きさ順に並び替えると「4、5、7、8、9」となり、中央値は7ということになりますね。
仮に観測値が「4、5、6、7、8、9」だった場合は、6と7の平均値(算術平均)である6.5が中央値になるわけですね。
一般に、算術平均の方が全てのデータを結果に反映させているため、中央値よりも平均値の方が「情報をフルに利用している指標」と見なすことができます。
ただし、算術平均に偏りがある場合には、中央値の方が有効な代表値になることもあります。
例えば、ある会社の社員9名の年収が400万円として、社長の年収が6400万円だとすると、その会社の平均年収は1000万円となりますが、これはその会社の実態を表しているとは言えないですよね。
このように、極端な外れ値が存在したり分布に大きな偏りがある場合、算術平均のように「すべての情報をフルに利用している」という特徴が足を引っ張り、実態に近い姿から遠ざかってしまうということになってしまうわけです。
こういう状況においては、大きすぎる値や小さすぎる値がいくつか含まれていたとしても、ほとんど影響を受けない中央値が有効になります。
先の例だと、年収の中央値は400万円になりますから、こちらの方が実態に近く、例えば会社を選ぶ際の有効な指標になりそうですね。
上記の通り、本問の観測値から算出される中央値は「7」であり「6.6」ではないことがわかります。
よって、選択肢①は誤りと判断できます。
② 幾何平均
④ 相乗平均
幾何平均は相乗平均とも称されるので、選択肢②と選択肢④は同じものを指しているということになります(こうした選択肢の示し方は珍しいですね)。
幾何平均(相乗平均)とは、各データの値を全てかけ合わせて、データ数の累乗根をとって得られたものです(以下が式になります)。
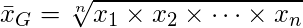
9×5×7×8×4を5乗根で計算するわけで、その数値は「6.3」となります。
幾何平均は「身長が毎年○○%ずつ伸びている」「貯金が毎年○○%ずつ伸びている」といった年の平均変化率を計算するときに用いられます。
例えば、ある会社の売り上げで、1年目が100%の売り上げ、2年目が‐50%の売り上げだったとしましょう。
これを算術平均で算出すると「25%」となりますが、幾何平均で算出すると「0%」になります。
上記の例を具体的に述べると、当初100の資金が1年目に100%ということで200になり、2年目には‐50%ですから200の半分で100になりますね(だから、幾何平均の0%が正しい。最初と変わっていないから)。
こうした例からもわかる通り、1年目では基準とする数字が100だが、2年目に基準とする数字は200になるわけで、こうした累積の変化を掴むのに幾何平均は優れているということになります。
上記の通り、本問の観測値から算出される幾何平均(相乗平均)は「6.3」であり「6.6」ではないことがわかります。
そもそも幾何平均を算出するためには「9×5×7×8×4」を手計算で算出した上に、5乗根をするという慣れていない人からするとなかなかの荒業をしないといけません。
幾何平均(相乗平均)の算出法を知っていれば「こんな無茶な計算を解答にすることはないだろう」とアタリを付けやすかろうと思います(他の選択肢の算出を楽にして、消去法で選択させるという意地悪問題である可能性もありますが…)。
以上より、選択肢②および選択肢④は誤りと判断できます。
③ 算術平均
算術平均とは、一般に「平均値」と呼ばれているものを指し、データの総和をデータ数で割った値となります。
エックスバー(Xの上に横棒)やMeanの頭文字をとってMという記号で表される代表値です。
今回は「9、5、7、8、4」というN=5のデータですから、(9+5+7+8+4)÷5を計算すればよいわけですね(ちなみにNとはnumberの頭文字です。母集団のサイズを表すときは大文字のN、その母集団から得たサンプル(標本)のサイズを表すときは小文字のnなので使い分けが大切です。この問題では5つのデータなのでN=5となります)。
この結果は「6.6」になります。
中央値の説明でも述べた通り、平均値を活用する場合にはデータの分布がどうなっているかを確認する必要があります。
外れ値があったり分布が偏っていると、真に役立つ代表値として機能しない場合も考えねばなりません(先述の平均年収の例がその最たるものですね)。
平均値に限らず、中央値も最頻値も、それぞれが最も活かせる状況(データ分布やデータの数)というものがありますから、それらをしっかりと把握して実際に活用できると良いですね。
さて、本問の観測値から算出される算術平均は「6.6」であることがわかります。
これは本問が提示している「6.6になる代表値」という条件に当てはまっていますね。
よって、選択肢③が正しいと判断できます。
⑤ 調和平均
調和平均とは、いくつかある広義の平均値のうちの一つであり、典型的には、率の平均が望まれているような状況で用いるのが適切とされています(具体的には、時速の平均や仕事算(ある仕事を終えるのにかかる時間が異なる人が数人あつまって共同作業をしたときに、仕事を終えるまでに要する時間はいくらかを求める問題)を求めるときによく使われます)。
より正確に表すと「各データの逆数の算術平均の逆数」で表されるのが調和平均です。
わかりにくいと思うので、具体的な例を出して考えてみましょう。
Aさんが学校へ行くときに、行きは時速10kmで走り、帰りは時速5kmで歩いて移動したとして、この時の平均時速を求めてみましょう。
算術平均だと「7.5(15÷2の結果ですね)」となりますが、これでは誤りになります(速度が違えば移動時間も異なってくるから)。
正確な算出の仕方を考えていきましょう
「自宅~学校」間の距離を「Xkm」とすると、往復で移動した距離は「2Xkm」となります。
続いて、行きと帰りの移動にかかった時間を考えてみましょう(時間=距離÷速度の式ね)。
それに基づけば、行きにかかる時間は「X/10時間」となり、帰りにかかる時間は「X/5時間」となります。
また、先ほどの「時間=距離÷速度」を変形すると、「速度=距離÷時間」であることもわかりますから、「平均時速=2X÷(X/10 + X/5)≓6.67」となり、平均時速は約6.67kmというのが答えになるわけです。
これを式にして表すと以下のようになります。
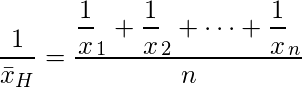
上記を見ればわかる通り、調和平均は算術平均よりも大きな観測値を受けにくく、平均値が小さくなるのが特徴でもあります。
さて、では改めて本問の値を調和平均で算出すると「6.0」になります。
これは本問の示している「6.6」という数字ではないことがわかりますね。
よって、選択肢⑤は誤りと判断できます。