統計の結果の解釈として最も適切なものを選択する問題です。
ほぼパス解析の結果で解いていきますが、正解にたどり着くには相関の結果も重要になってきます。
問59 ストレッサー、ネガティブな自動思考(以下「自動思考」という)及び抑うつ反応の3つの変数を測定した。ストレッサーは、調査前の出来事を測定した。変数間の相関係数を算出したところ、ストレッサーと抑うつ反応の相関係数は0.30、ストレッサーと自動思考の相関係数は0.33、自動思考と抑うつ反応の相関係数は0.70 で、いずれの相関係数も有意であった。パス解析を行ったところ、ストレッサーから自動思考への標準化パス係数は0.31で有意であり、自動思考から抑うつ反応への標準化パス係数は0.64で有意であり、ストレッサーから抑うつ反応への標準化パス係数は0.07で有意ではなかった。
以上の結果から解釈可能なものとして、最も適切なものを1つ選べ。
① 自動思考は、抑うつ反応に対して影響を与える説明変数ではない。
② 抑うつ反応は、ストレッサーに対して影響を与える説明変数である。
③ ストレッサーは、抑うつ反応に対して自動思考を介して影響を与えている。
④ 自動思考が根本的な原因として、ストレッサーと抑うつ反応の両方を説明している。
⑤ 抑うつ反応に対して、ストレッサーと自動思考は対等に説明する変数となっている。
解答のポイント
パス解析の概要を把握している。
必要な知識・選択肢の解説
まず「パス解析」を説明するための前提として、重回帰分析について説明をしていきましょう。
重回帰分析とは、従属変数のばらつきを、いくつかの独立変数によって説明したり、予測するための統計的手法のことです。
一つの従属変数に対して、一つの独立変数によって説明・予測するのを「単回帰分析」と呼びます(重回帰分析は独立変数が複数あります)。
例えば、身長を体重という一つの説明変数から予測するのは単回帰分析であるのに対して、重回帰分析は身長を体重、年齢、性別など複数の説明変数から予測します。
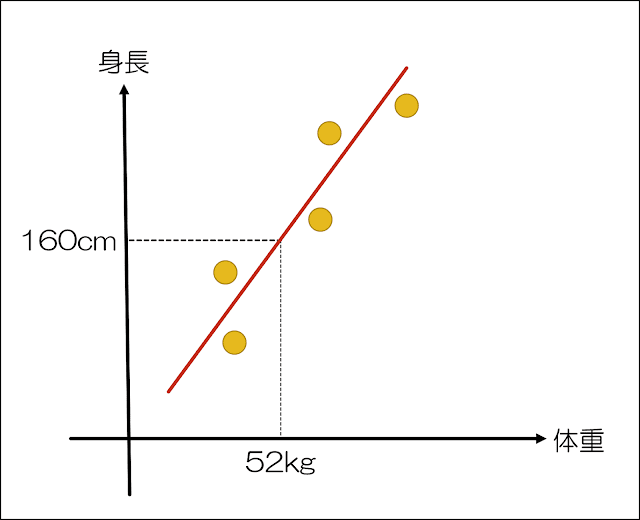
上記のような線を「回帰」と呼び、重回帰分析(単回帰分析も)は、こうした回帰直線を求めるのでその名が付いており、複数の独立変数から従属変数を説明・予測する統計手法であり、重相関係数(いくつかの独立変数全体が従属変数に与える影響を示した値)や決定係数(回帰分析によって求められた目的変数の予測値が、実際の目的変数の値とどのくらい一致しているかを表している指標。単純に言えば、決定係数が0.7ならその独立変数で従属変数の70%を説明できるということ)を指標として評価するものです。
このように、重回帰分析(重回帰モデル)は、独立変数を原因、1つの従属変数を結果と見なした因果モデルと言えますが、現実はもっと複雑であることが多いですよね。
例えば、欠席・予習・成績・知識・興味という因子があるとして、①興味は低い欠席率と予習を介して、成績を高める、②知識があると成績を高めるが、予習を短縮させる、③知識と興味は相関する、などという予想ができます。
このように、分析者が考えた因果モデルに基づく分析を「パス解析」と呼びます。
重回帰分析では各独立変数から従属変数への一方向の因果のみを仮定するのに対し、パス解析では変数間に自由に因果関係を仮定してモデルをつくることが可能になります。
加えて、重回帰分析では変数ごとに相関関係が生まれるモデルには不適な場合がありますが、パス解析ではそうした相関関係(1つが変化すれば応じてもう1つも変化するという関係性)も説明が可能です。
パス解析においては、他の変数の寄与を受ける変数(要は1回以上、因果の「果」になる)をすべて「従属変数:内生変数」と呼び、それ以外(1回も「果」にならない、完全な「因」)を「独立変数:外生変数」と呼びます。
パス解析の構造上、不可欠なことは、内生変数には必ず「残差」という、研究者が挙げた要因以外の諸要因のことであり、この残差からパスを受ける必要もあるわけです。
問題文にある「標準化パス係数」ですが、まず「パス係数」は変数間の相関関係および因果関係を表す値です。
パス係数には標準化解と非標準化解の2種類があり、標準化解はすべての観測変数と潜在変数の分散を1に基準化して求めたときの値、非標準化解は基準化しないそのままのデータについて求めたときの値です(この辺は解説にあまり関係しませんが念のため)。
とりあえず上記の理解を踏まえ、各選択肢の解説に入っていきましょう。
① 自動思考は、抑うつ反応に対して影響を与える説明変数ではない。
② 抑うつ反応は、ストレッサーに対して影響を与える説明変数である。
③ ストレッサーは、抑うつ反応に対して自動思考を介して影響を与えている。
④ 自動思考が根本的な原因として、ストレッサーと抑うつ反応の両方を説明している。
⑤ 抑うつ反応に対して、ストレッサーと自動思考は対等に説明する変数となっている。
まずは本問の相関関係やパス解析の結果を図で示しましょう。
本問の解説は以下の図を踏まえつつ解いていきますから、全ての選択肢をいっぺんに説明していくことにします。
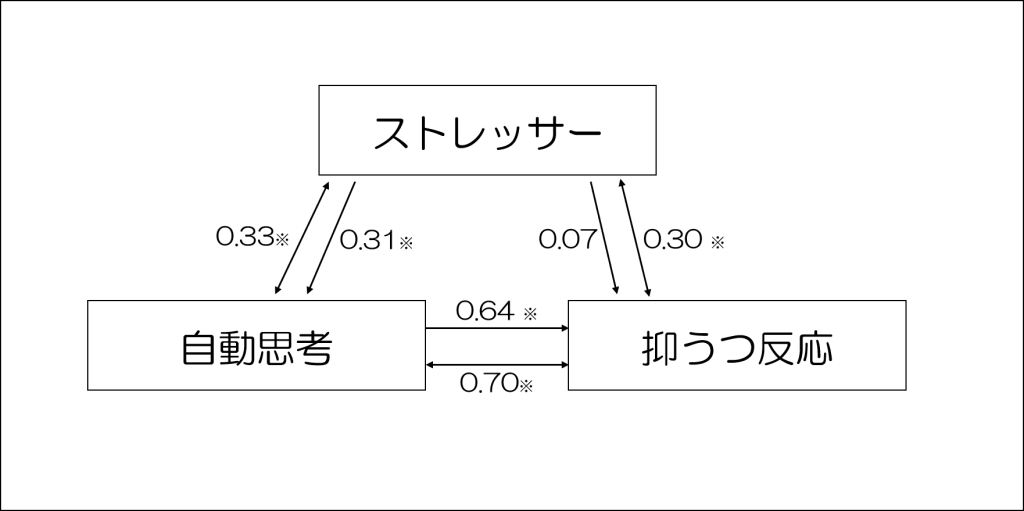
言うまでもないかもしれませんが、数字の後ろに「※」がついているところが有意だったよ、という意味です(有意水準が示されていませんから、とりあえずわかりやすくするためのものと考えておいてください)。
また、双方向の矢印(↔)に関しては相関係数を、単方向の矢印(→)に関しては標準化パス係数を表します。
これを見ながら各選択肢の解説に入っていきましょう。
まず選択肢①の「自動思考は、抑うつ反応に対して影響を与える説明変数ではない」についてですが、こちらの「影響を与える」というのは標準化パス係数を見る必要があります。
相関関係についてはすべて有意となっていますが、相関であれば「影響を与える」という捉え方にはなりません(片方が上がる(下がる)と片方が上がる(下がる)、ということ以上は言えない)。
それを踏まえて選択肢①の内容を見ると、これでは自動思考から抑うつ反応に標準化パス係数が伸びて有意になっていることと矛盾しますね。
同じような内容として、選択肢②の「抑うつ反応は、ストレッサーに対して影響を与える説明変数である」がありますが、ストレッサーから抑うつ反応に伸びている標準化パス係数は有意ではありませんから、この内容も問題文と合致しません
さらに、選択肢③の「ストレッサーは、抑うつ反応に対して自動思考を介して影響を与えている」を解説していきましょう。
ここで重要なのは、以下の点になります。
- ストレッサー→自動思考の標準化パス係数が有意である。
- 自動思考→抑うつ反応の標準化パス係数が有意である。
- ストレッサー→抑うつ反応の標準化パス係数は有意ではない。
- ストレッサーと抑うつ反応は相関係数は有意である。
1~3だけであれば「ストレッサーは抑うつ反応に対して自動思考を介して影響を与えている」ということはできません。
ですが、ここで重要なのは4のストレッサーと抑うつ反応の相関が有意であることであり、これは「ストレッサーが上がると、抑うつ反応も上がる」ということが示されているわけです。
ストレッサーが直接は抑うつ反応に影響を与えていないのは3から明らかですから、4の相関関係を踏まえれば、選択肢③の「ストレッサーは、抑うつ反応に対して自動思考を介して影響を与えている」と見なすのが妥当なわけですね。
本問では、ほとんどがパス解析の結果を使うのですが、本選択肢の「自動思考を介して」という間接的な影響を示唆するために相関係数の結果が使われるわけですね。
では選択肢④の「自動思考が根本的な原因として、ストレッサーと抑うつ反応の両方を説明している」について考えていきましょう。
こちらはそもそも「自動思考が根本的な原因として」と考えるのが難しいことがわかりますね。
「ストレッサー→自動思考」というパスが出ている以上、しかもそれが有意である以上、少なくともここの関係性としてはストレッサーが自動思考に影響を与えているということになります。
選択肢の内容通りであれば、自動思考からストレッサーおよび抑うつ反応にパスが出ているはずですが、本問ではそうなってはいませんね。
ですから、自動思考をストレッサーと抑うつ反応の両方を説明しているという捉え方は誤りであることがわかるはずです。
最後に選択肢⑤の「抑うつ反応に対して、ストレッサーと自動思考は対等に説明する変数となっている」についてです。
こちらについては、抑うつ反応に対して自動思考は説明する変数となっていますが、選択肢③でも述べた通り、ストレッサーは間接的な影響にとどまっており、自動思考と対等に説明する変数と見なすのは無理があります。
選択肢⑤の通りであれば、ストレッサーと自動思考の両方からパスが抑うつ反応に対して出ているはずですよね。
以上より、選択肢①、選択肢②、選択肢④および選択肢⑤は不適切と判断できます。
また、選択肢③が適切と判断できます。