各統計手法が「いったい何をしているのか?」に関する根本的な理解が問われています。
単純なようで、中途半端な理解を許さない問題と言えますね。
問81 個体を最もよく識別できるように、観測変数の重みつき合計得点を求める方法として、最も適切なものを1つ選べ。
① 因子分析
② 重回帰分析
③ 主成分分析
④ 正準相関分析
⑤ クラスター分析
解答のポイント
各統計手法の特徴を把握している。
選択肢の解説
① 因子分析
まずは具体例から挙げていきましょう。
ある国の国民性に関するイメージについて調査を行う際、アンケート項目は以下のように設定されたとします。
- 時間を守りそうか
- メールをすぐに返しそうか
- 整理整頓が好きそうか
- 笑顔が多そうか
- 自分の意思を正確に伝えることが得意か
- 相手の意図を正確に汲み取るのがうまいか
このように、各項目は我々が持つイメージについて独立に問うものではありますが、背景には共通する評価軸が存在している可能性も考えられるはずです。
このように観測された変数(ここではアンケートの質問項目に対する評価点)に影響を与えているとされる、目に見えない要因(ここでは「几帳面さ」および「コミュニケーション能力」のような評価軸)で説明する統計的手法を「因子分析」といいます。
心理学では通常、観測されたデータから目に見えない要因(因子)について議論することが多く、因子分析は広く用いられている手法と言えます。
因子分析については「公認心理師 2018追加-6」において、「きっと世の中に存在するに違いない「データの背後に潜む説明変数(独立変数)」を見つけ出す分析手法」と説明していますが、これは上記の説明の言い方を変えているだけで、同じことを言っているのがわかると思います。
因子分析において、観測変数(上記でいうアンケート項目)はそれぞれの共通因子(上記でいう「几帳面さ」および「コミュニケーション能力」のような評価軸)から影響を受けており、この影響の度合いは「因子負荷量」と表現されます。
このように因子分析とは、観測変数の背後にある構成概念(因子)を測定する手法であり、因子負荷量などを求めることで解釈を行っていきます。
本問の「個体の識別」という目的に沿うものではないことがわかりますね(もしもわかりにくければ、次の選択肢の解説と併せて見てみるとわかりやすくなるでしょう)。
以上より、選択肢①は不適切と判断できます。
③ 主成分分析
上記の因子分析とよく似た手法が主成分分析です。
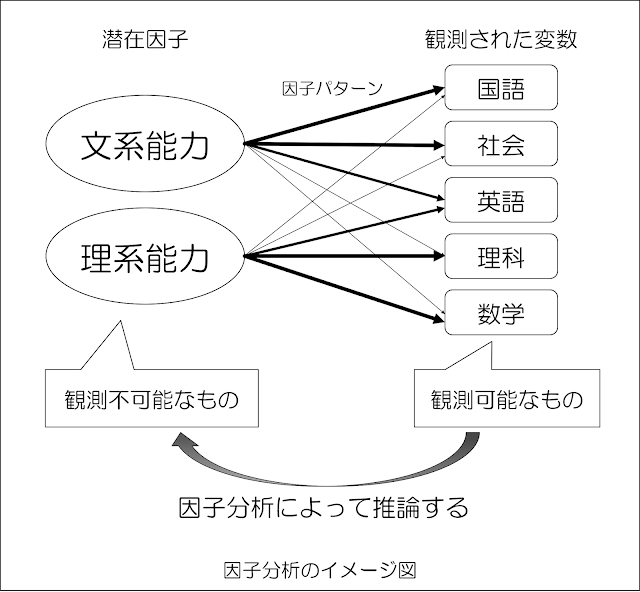
例えば、国語、数学、理科、社会、英語の5教科があるとして、この5教科の背景にある共通因子を見つけるのが「因子分析」になります。
観測された変数である5教科の得点は、共通(潜在)因子(文系能力・理系能力)から影響を受けていることになり、上記の矢印の太さが影響の度合いである「因子負荷量」の大小を表現していると考えてください。
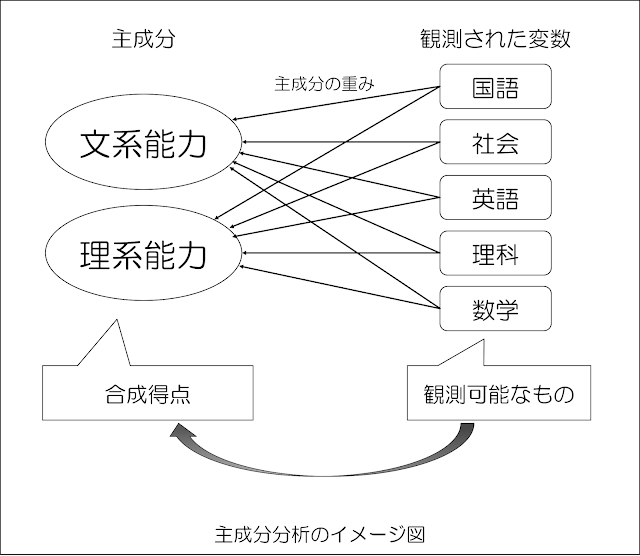
これに対して、主成分分析では「情報を集約すること」が目的になります。
主成分分析では、もともとのデータ(観測された変数)に存在する情報を、新たな軸(成分)で記述するための数学的手法です。
上記のように、潜在因子からの影響を考える「因子分析」とは異なり、「主成分分析」では観測された変数が共有する情報を合成変数として集約するので、図の矢印の向きが逆になっていることがわかりますね。
こうした「主成分分析」の特性上、手元にある多次元のデータから何らかのパターンを見つけ出したいとき、つまりデータ駆動で研究を進めたい場合などに、軸の解釈に注意しながら活用すると有効な方法となります。
もう少しかみ砕いて述べると、主成分分析を用いるのは主として「合成得点を算出したいとき」になります。
例えば、5教科のテスト結果が分かっているとき、5教科の得点を合計して総合得点を算出しますね。
ですが、国語の平均点が20点、数学の平均点が70点だった場合、数学が得意な生徒が総合得点で上位を占めることになってしまい、不公平な結果となります。
このようなときには主成分分析を用いて、各教科の点数に「重みづけをして」をすることで合成得点を算出すると、より実力に応じた結果が見えやすくなります。
つまり、主成分を算出する(主成分=重みつき合計得点)ことで、それぞれの個体の持っている力や特性を識別しやすくすることができるということになりますね。
以上より、本問の「個体を最もよく識別できるように、観測変数の重みつき合計得点を求める方法」は主成分分析であると考えるのが妥当です。
よって、選択肢③が適切と判断できます。
② 重回帰分析
重回帰分析とは、従属変数のばらつきを、いくつかの独立変数によって説明したり、予測するための統計的手法のことです。
一つの従属変数に対して、一つの独立変数によって説明・予測するのを「単回帰分析」と呼びます(重回帰分析は独立変数が複数あります)。
例えば、身長を体重という一つの説明変数から予測するのは単回帰分析であるのに対して、重回帰分析は身長を体重、年齢、性別など複数の説明変数から予測します。
まずは単回帰分析のやり方を踏まえて、重回帰分析を理解していきましょう。
例えば、身長と体重の以下のような表があるとしましょう。
この時、Aさん~Eさんの身長体重がわかっているので、そこからFさんの身長を予測しようとします。
その結果、上記のような赤線を引くことができましたので、そこから「体重52kg」は「身長160cm」であると推測することができますね。
これを「y=ax+b」と表現します。
yは従属変数(身長)であり、xは独立変数(体重)、aは傾きで定数が入り、bは切片で同じく定数が入ります。
こうした直線を描くことができれば、2変数間の関係を表現できていることになり、仮説が統計的に検証されたと考えることができます。
これが単回帰分析の基本的な考え方になります。
重回帰分析では、独立変数が複数になってきます。
例えば、身長という従属変数を、体重と足のサイズという2つの独立変数で予測しようとするときには「y=a1x(体重)+a2x(足のサイズ)+b」となるわけです。
上記の赤線を回帰(重回帰)分析では「回帰」と呼びますが、この回帰モデルの当てはまりの良さ、つまり、得られた回帰式が従属変数の変動をどの程度よく説明しているかは「重相関係数」や「決定係数」を指標として評価することができます。
このように、重回帰分析は本問の「個体を最もよく識別できるように、観測変数の重みつき合計得点を求める方法」という説明にはそぐわないことがわかりますね。
重回帰分析は、回帰直線を求めることで、複数の独立変数から従属変数を説明・予測する統計手法であり、重相関係数や決定係数を指標として評価するものです。
以上より、選択肢②は不適切と判断できます。
④ 正準相関分析
選択肢②の重回帰分析は1つの従属変数のばらつきを、複数の独立変数によって説明・予測するための統計的手法でしたが、これに対して、複数の従属変数に対して、複数の独立変数が影響することを調べる手法を正準相関分析と呼びます。
例えば、体力測定を行い、身長・体重・上肢長・下肢長の変数群(独立変数群)が、握力・背筋力・垂直跳びの変数群(従属変数群)にどのように関係するか知りたいときに、いくつかの方法が考えられます。
その一つは、2種類のグループについて総当りで相関係数を求め、それらを総合的に評価する方法です。
上記の例の場合、4×3=12種類の単相関係数が求められることになります。
そして同じグループの臨床検査値間には相関があることを考慮した上で、これら12種類の単相関係数を検討し、相関関係を総合的に評価する必要がありますが、これは正直かなり面倒で難しい作業になります。
もう一つの方法は、重相関係数を利用するというやり方です。
重相関係数は、一つの項目と複数の項目の間の相関性を表す指標ですから、2種類のグループのうち数が少ない方の項目の一つひとつについて、もう一方のグループとの重相関係数を求めることによって評価すべき相関係数の数を減らすことができます。
しかしこの方法でも、独立変数同士の相関は山勘で評価することになりますから、これでは何となく中途半端になってしまいます。
そこで用いるのが正準相関係数になります。
こちらは言わば「グループ間の相関」について考える方法であり、2つのグループの相関関係を1つの相関係数で要約できます。
そのようなグループ間の相関のことを正準相関といい、正準相関の程度を表す指標のことを正準相関係数と呼びます。
この正準相関係数を求める手法のことを「正準相関分析」と呼び、これは重相関係数と重相関分析を拡張した手法に相当します。
各方法のイメージ図は以下のような感じです。
心理学分野では、心理的因子を複数のアンケート項目によって評価し、それらの心理的因子がお互いにどのように関連しているかを検討することがあります。
すなわち、複数の指標を総合して検討することが多く、その意味で正準相関分析は心理学分野で活用されやすい統計手法と言えます。
このように、正準相関分析は本問の「個体を最もよく識別できるように、観測変数の重みつき合計得点を求める方法」という説明にはそぐわないことがわかりますね。
正準相関分析は、複数の従属変数に対して、複数の独立変数が影響することを調べる手法です。
以上より、選択肢④は不適切と判断できます。
⑤ クラスター分析
判別すべき群があらかじめ与えられていない場合に、群を構成する手法、すなわち似た個体同士は同一群、隔たる個体同士は異なる群に属するように個体を群分けする手法を「クラスター分析」と呼びます。
簡単に言えば、様々な特性をもつ対象を類似性の指標を元にグルーピングする手法ですね(この「類似性」というのがクラスター分析のキーワードかなと思います)。
例えば、世界各国の100個のチョコレートを試食したときに「どのくらい甘いか」「どのくらい苦いか」を0~100で評価して、ビジュアルアナログスケールで尋ねたとします。
その結果として、以下のようなデータが得られたとします。
このようにしてみてみると、「甘味も苦みも強いチョコ」「甘味が強いチョコ」「苦みが強いチョコ」「甘味も苦みも弱いチョコ」という4つのまとまりに分かれているように見えますね。
このような時、「類似性」を基準として統計的に対象を分類していくクラスター分析を用いて、まとまりについての検証を行うことができます。
クラスター分析には大きく分けて、階層的クラスター分析と非階層的クラスター分析があります。
階層的クラスター分析では、個々のデータを1つのクラスターとしてみなし、類似性に基づいてクラスターを結合していき、この手続きを最終的に1つのクラスターが形成されるまで続けます。
一方で、非階層的クラスター分析では、分析者が事前にクラスター数を設定し、データをそのクラスター数に分ける方法です。
以上のように、クラスター分析は本問の「個体を最もよく識別できるように、観測変数の重みつき合計得点を求める方法」という説明にはそぐわないことがわかりますね。
クラスター分析は、変数について効果的な類似性を探す手法と言えます。
よって、選択肢⑤は不適切と判断できます。