実験計画についての理解を問う内容になっています。
主効果、交互作用などの統計用語の理解、独立変数と従属変数を同定する力が必要になってきます。
問59 石けんの香りが机を清潔に保とうとする行動に影響を与えるかについて実験を行った。香りあり条件と香りなし条件を設けて、机の上の消しくずを掃除する程度を指標として検討した。その結果、全体的には香りあり条件と香りなし条件の差が検出されなかったが、尺度で測定された「きれい好き」得点が高い群は、全体として「きれい好き」得点が低い群よりもよく掃除をした。さらに、高い群では香りあり条件と香りなし条件の差は明瞭でなかったが、低い群では、香りあり条件が香りなし条件よりも掃除をする傾向が顕著に観察された。
この実験の結果の理解として、正しいものを1つ選べ。
① 交互作用はみられなかった。
② 実験要因の主効果は有意であった。
③ 「きれい好き」要因の主効果は有意ではなかった。
④ 実験要因の主効果と交互作用が有意であった可能性が高い。
⑤ 「きれい好き」要因の主効果と交互作用が有意であった可能性が高い。
解答のポイント
問題文から実験計画の構造を掴むことができる。
主効果・交互作用の有無を判断することができる。
選択肢の解説
① 交互作用はみられなかった。
② 実験要因の主効果は有意であった。
③ 「きれい好き」要因の主効果は有意ではなかった。
④ 実験要因の主効果と交互作用が有意であった可能性が高い。
⑤ 「きれい好き」要因の主効果と交互作用が有意であった可能性が高い。
まずは問題に入る前に、基本的な用語の意味を確認しておきましょう。
「主効果」と「交互作用」について理解しておくことが大切です。
実験計画法において、2要因以上の独立変数の効果を調べるために実験計画を組み、統計的検定を行うとき、他の要因のすべての条件を併せた当該の要因の条件間でデータの値に差があるとき、その要因の「主効果」があると表現します。
ちょっと分かりにくいでしょうから、もっと砕けた言い方で表現すると、それぞれの独立変数がそれぞれ「独自」に従属変数へ与える単純効果のことを指すわけです。
また、一方の要因の条件によって他方の要因の効果(データの値の条件間の差の方向や程度)が異なるとき、それらの要因の間には(従属変数に対して)「交互作用」があると表現します。
こちらもちょっと分かりにくいかもしれないので、言い換えると、2要因以上が設定されている状況では、ある要因の効果が他の要因によって左右されることがあり、これを両者の間に「交互作用」があると考えるわけです。
記憶の研究において、具体性のある単語の方が忘却しにくいという知見があり、この効果は経過時間が長いほど顕著になるとします。
つまり、「単語の具体性」という要因は、「経過時間の長さ」という要因によって規定されるということであり、この状況を「交互作用がある」と見なすわけです。
独立変数を組み合わせた場合の複合効果のことを「交互作用」と呼ぶわけですね。
さて、ここまでが解くための前提となります。
これを理解した上で、次は問題に入っていきましょう。
問題を解くにあたって、まず必要なのは本問の実験計画の構造を掴むことです。
まずは本問の「独立変数」と「従属変数」について理解しましょう。
本問における「独立変数」は以下の2つになります。
- 石けんの香り要因:あり・なしの2水準
- きれい好き度要因:高い・低いの2水準
続いて「従属変数」ですが、これは「机の上の消しくずを掃除する程度」になりますね。
そして、この実験計画は分散分析による検定を用いていると言えます。
まずは文章からこれを把握することが肝要です。
では、ここからは問題を解いていくことにしましょう。
本問の問題文は丁寧に作られています。
問題文の見るべきポイントは以下のように区切ることができます。
- 【香りあり条件と香りなし条件を設けて、机の上の消しくずを掃除する程度を指標として検討した。その結果、全体的には香りあり条件と香りなし条件の差が検出されなかった】
- 【が、尺度で測定された「きれい好き」得点が高い群は、全体として「きれい好き」得点が低い群よりもよく掃除をした。】
- 【さらに、高い群では香りあり条件と香りなし条件の差は明瞭でなかったが、低い群では、香りあり条件が香りなし条件よりも掃除をする傾向が顕著に観察された】
上記の1~3を順番に見ていけば、この問題を解くことができます。
特に1と2を区切れるかが重要です(一つの文章の真ん中で切らなきゃいけないのがちょっとややこしい)。
まず、上記の1を見ていきましょう。
【香りあり条件と香りなし条件を設けて、机の上の消しくずを掃除する程度を指標として検討した。その結果、全体的には香りあり条件と香りなし条件の差が検出されなかった】
これを図で表すと以下のようになります。
石けんの「香りあり群」と「香りなし群」では、従属変数(掃除をする頻度)に変わりがないわけですから、上記のような図になるのがわかるでしょう。
ここに差がないわけですから、「石けんの香り要因」の主効果は無いということになります。
意外と混乱しやすい点として、これを考えるときに「きれい好き度要因はどうなるの?」ということかもしれません。
実験に取り上げた因子が複数ある時は、分散比から判断して、影響のないと思われる因子を誤差にまとめて表示し、これを「プーリング」と呼びます。
とりあえず「石けんの香り要因」だけにまとめてしまって、「石けんの香り要因」と従属変数との関係を見ていくという手続きを行うということです。
続いて、上記の2の検証に移りましょう。
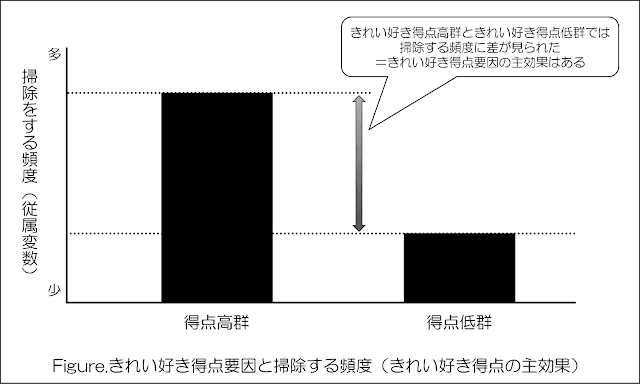
【が、尺度で測定された「きれい好き」得点が高い群は、全体として「きれい好き」得点が低い群よりもよく掃除をした。】
こちらを図にすると以下の通りです。
きれい好き得点の高群と低群で、掃除をする頻度(従属変数)に差があるわけですから、上記のような図表現になるのがわかりますね。
このことから「きれい好き得点要因」の主効果は有意であった可能性が高いと言えるわけですね。
さて、最後に上記の3の検証を行いましょう。
【さらに、高い群では香りあり条件と香りなし条件の差は明瞭でなかったが、低い群では、香りあり条件が香りなし条件よりも掃除をする傾向が顕著に観察された】
交互作用の意味として「ある要因の効果が他の要因によって左右されること」とわかっていれば、この文章から「交互作用がある」と考えることができると思います。
ただ、これだけでは少しわかりにくい人もいるかもしれないので、ちょっと別方向の考え方も入れておきましょう。
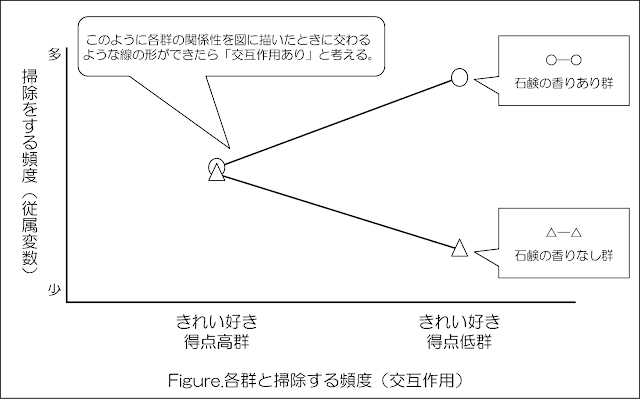
少々複雑ですが、【さらに、高い群では香りあり条件と香りなし条件の差は明瞭でなかったが、低い群では、香りあり条件が香りなし条件よりも掃除をする傾向が顕著に観察された】を図にすると以下のようになります。
「きれい好き得点の高群」では「石けんの香りあり群」も「石けんの香りなし群」も差はないわけですから、図の左側の表現になりますね。
そして、「きれい好き得点の低群」では「石けんの香りあり群」の方が「石けんの香りなし群」よりも顕著に掃除をするので、図の右側の表現になるわけです。
交互作用を確認する時には、上記のような図を描いてみるのが手っ取り早いです。
なぜなら「交互作用が有意」である時には、上記の線は基本的に「交差する」からです。
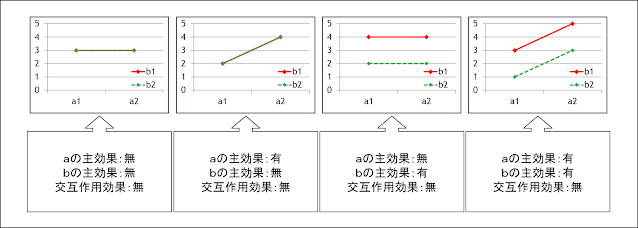
わかりにくい方は以下の図を参考にしてみてください。
上記の図では、いずれの線も「交差」していないことがわかりますね。
こういう場合には「交互作用なし」になります。
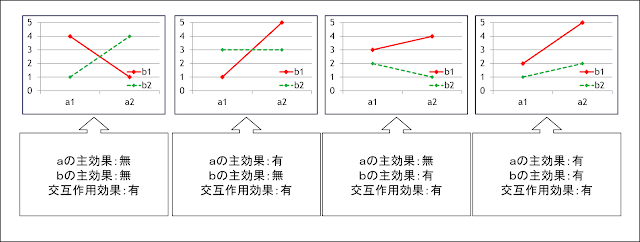
これに対して、以下の図を確認してみましょう。
この図では、いずれの場合でも線が「交差する」のがわかると思います。
右二つは交差していませんが、こういう時の見方は「両線を伸ばした時に交差するか否か」で判断します。
右二つも線分を伸ばしていけば交差することがわかりますから、こういう時には「交互作用あり」となるのです。
このことを踏まえれば、本問の【さらに、高い群では香りあり条件と香りなし条件の差は明瞭でなかったが、低い群では、香りあり条件が香りなし条件よりも掃除をする傾向が顕著に観察された】では、線が交差することがわかりますから、交互作用があると見なすことができますね。
ここまでをまとめると、以下のようになります。
- 「石けんの香り要因」の主効果は認められない。
- 「きれい好き得点要因」の主効果は認められる。
- 交互作用ありと見なすことができる。
これらを導くことができれば、本問の正解にたどり着くことができます。
交互作用ありなので、選択肢①は誤りです。
選択肢②や選択肢④にある「実験要因」とは、「石けんの香り要因」と「きれい好き得点要因」の両独立変数を指していますので、間違いであることがわかりますね(石けんの香り要因は有意ではないから)。
「きれい好き得点要因」の主効果は認められるので、選択肢③は誤りですね。
以上より、「きれい好き得点要因」の主効果が認められ、また、交互作用もありと見なしている選択肢⑤が正しいと判断することができます。