パーソナリティ検査というよりも、質問紙を作成するときに必要な統計的知識について問われています。
各概念に関する基本的な理解を問うてはいますが、学ぶ上では理論的にも理解するよう努めると良いでしょう。
問12 質問紙法を用いたパーソナリティ検査について、正しいものを1つ選べ。
① 検査得点の一貫性のことを妥当性という。
② α係数は、検査項目の数が多いほど、低い値をとる。
③ 再検査法では、2時点の検査得点間の相関係数を用い、検査の安定性をみる。
④ 検査が測定しようとしているものを正しく測定できている程度のことを信頼性という。
⑤ 検査得点の分散に占める真の得点の分散の割合が高いほど、検査結果の解釈が妥当になる。
解答のポイント
質問紙作成にまつわる統計的知識について理解していること。
選択肢の解説
① 検査得点の一貫性のことを妥当性という。
④ 検査が測定しようとしているものを正しく測定できている程度のことを信頼性という。
これらの選択肢は「信頼性」と「妥当性」に関する理解を問うています。
信頼性・妥当性の考え方さえ知っておけば、真っ先に正誤判断ができる選択肢ですので、絶対に落としたくないものと言えますね。
まず、信頼性とは「同一の個人に対して同一の条件の元で同一のテストを繰り返し実施したとき、一貫して同一の得点が得られる程度」のことを指します。
簡単に言えば、「何回やっても同じ結果になるよ」「テストの結果が安定していると、一貫しているよ」というのが信頼性で、それを数値化したのが「信頼性係数」という指標になります。
信頼性係数は1つではなく、さまざまな視点から算出されますし、その算出方法も視点によって変わってきます。
その辺に関しては、別選択肢で述べていきましょう。
また、妥当性とは「テスト得点の解釈とそれに基づく推論の正当性の程度」のことを指します。
わかりにくいので、もっと以前から言われている定義で述べると「テストが測定を目指したものを実際に測定している程度」ということになります。
要は「測りたいものが測れているよ」という程度を測る指標ということですね。
妥当性は信頼性と異なり、テスト得点自体の性質ではなく、測定の目的との関係で評価が変わってくるものになります。
以上より、本選択肢の表現を用いて捉えなおすと、「検査得点の一貫性のこと」を信頼性と呼び、「検査が測定しようとしているものを正しく測定できている程度のこと」を妥当性と呼びます。
よって、選択肢①および選択肢④は誤りとであると判断できます。
② α係数は、検査項目の数が多いほど、低い値をとる。
まずα係数とは、信頼性の指標の一つである「内的整合性」を示すものです。
信頼性とは「テストにおける回答の安定性・一貫性」であり、もっと噛み砕いて言えば「だいたいいつも同じような結果が得られる」ということになります(もちろん同じ対象、同じ傾向をもつならば、ですよ)。
そして、その信頼性を数値化した指標が「信頼性係数」であり、α係数は信頼性係数の一つと言えます(この点については他の選択肢でも詳しく述べてありますので、そちらに譲ります)。
α係数が示す「内的整合性」についても理解しておきましょう。
内的整合性とは、その質問紙の検査項目の安定性・一貫性を示す概念です。
つまり、検査の尺度内部で回答のバラツキがないことを意味しており、尺度内の各項目が構成概念を同じように測ることができて、バラツキがなく、一貫していることを信頼性が高いとする概念のことですね。
もう少し砕いて言うと「内的整合性によって作成された検査(YG性格検査など)は、質問項目の重みが一定である」ということになります。
図にすると以下のようなイメージです。
このように、内的整合性は質問項目の一貫性・安定性を示す指標であることがわかると思います。
この内的整合性を示す方法として、古くから使われているのが「折半法」でした。
折半法は、質問項目を折半(つまり2つに分ける。奇数と偶数に分ける奇遇法とか)して、その2つの得点の相関を見るという方法です。
ただ、折半法では折半の方法が無数にあるので、もっと厳密に考えうる折半方法すべてに関して信頼性係数を求め、それを平均したのが「α係数」になります。
α係数は、クロンバックによって発見されたため「クロンバックのα係数」とも呼ばれます。
本選択肢の「検査項目の数が多いほど、低い値をとる」か否かについては、このα係数の計算式を理解しておくことが重要になります。
難しい数式を抜きにしてα係数の算出方法を示すと以下の通りです。
α係数={項目数÷(項目数-1)}{1-(各項目の分散の和÷合計得点の分散)}
要するに、α係数は項目数と項目の分散、尺度得点の分散から計算されるということです。
なお、「各項目の分散の和」とは、例えば、10個の質問がある質問紙を10人にした場合、第1問に関する10人分の回答が得られますから、その回答のバラつき具合(=分散)を算出したものとなります(それが10問分あるということ)。
また「合計得点の分散」とは、被検査者毎の合計点があり、それのバラつき具合(=分散)になります。
この計算式踏まえると、以下の事態にはα係数が大きくなることがわかります。
- 合計点の分散を大きくする(被検査者の回答が、被検査者同士バラバラになる)。
- 各項目の分散の合計を小さくする(ある項目に関して、被検査者全員が同じような回答をする)。
- 項目数を増やす。
1と2は矛盾し合いますが、3は簡単ですね。
尺度平均値の分散は項目数に応じて小さくなっていくので、項目数が増えれば自然とα係数は高くなっていきます。
ただし、数式まで覚えておくというのは、好きな人以外にはなかなか過酷な話だと思います。
そこで「α係数は項目数が多いと高くなりがちで、項目数が少ないと低くなる傾向にある」と単純に覚えておくだけでもよいだろうと思います。
ちなみに、通常項目数が多いほどα係数は高くなるはずですが、項目数を減らしているのにα係数が高くなるというのは、この項目による測定の信頼性に疑問があることになります。
例えば、項目内容が似通っている場合、項目数が少なくてもα係数が高くなるということも起こります。
しかし、その場合は「同じことしか聞いていない」ということになり、信頼性が高くなったとしても、今度は妥当性の面で問題が生じると見なすことができます。
以上より、選択肢②は誤りと判断できます。
③ 再検査法では、2時点の検査得点間の相関係数を用い、検査の安定性をみる。
信頼性を示す指標としては、以下のものが挙げられています。
- 再現性(安定性):検査結果の再現性が高く、同一の検査対象であるなら何度測定を繰り返しても同じような測定値が得られるほど、安定しており信頼性が高いとする概念のこと。
- 等価性:検査が測ろうとしている構成概念と同じ、あるいは似通った概念を測る他検査と一定の関係が認められれば、信頼性が高いとする考え方の概念のこと。
- 内的整合性(内的一貫性):検査の尺度内部で回答のバラツキがないことを意味する。尺度内の各項目が構成概念を同じように測ることができて、バラツキがなく、一貫していることを信頼性が高いとする考え方の概念のこと。
さて、この3つはあくまでも信頼性を見るための「概念」にすぎません。
この各概念に沿って、実際に信頼性を測定する「方法」が必要になり、「方法」によって検出されるのが「信頼性係数」となります。
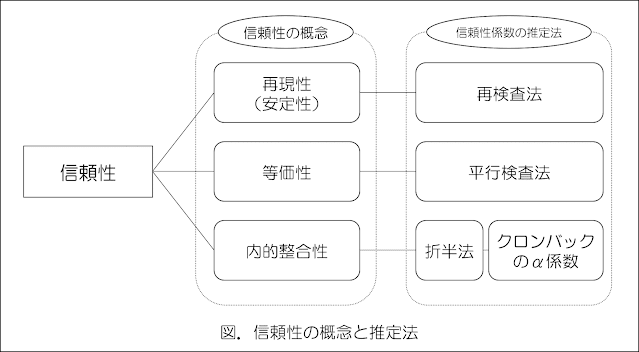
「概念」と「方法」の組み合わせについては以下の通りです。
このように、信頼性の概念ごとに、それに合う推定法が示されているのがわかります。
各推定法に関しては以下の通りです。
- 再検査法:再現性(安定性)によって信頼性を推定する方法。一定期間(2週間から1ヶ月)をおいて、同じ検査を行い、その二つの得点間の相関係数を信頼性係数とする。
- 平行検査法(代理検査法):等価性によって信頼性を推定する方法。測定したい検査と、項目数・質問内容の難易度・測定したい構成概念・分布・平均値・分散などがほぼ等しい検査を作成もしくは使用して、その二つの検査間の相関係数を信頼性係数とする。
- 折半法:内的整合性(内的一貫性)によって信頼性を推定する方法。同一の対象に2回検査を実施することが困難な場合もある。そこで、例えば、ある検査を偶数項目と奇数項目に折半し(奇遇法)、二つの尺度とみなしてその相関係数を信頼性係数とする。このやり方を「スピアマン・ブラウンの公式」と呼ぶ。
- クロンバックのα係数:内的整合性(内的一貫性)によって信頼性を推定する方法。例えるなら項目群の可能なすべての組み合わせについて相関係数を算出して平均を求めたような感じ。そのため、折半法をより一般化した推定方法と言える。α係数は0~1の値を取り、1に近づくほど信頼性が高い。ただし、このやり方だと、項目の中に似通ったものがあるほど、信頼性係数は高くなってしまう。項目数を増やすほどに信頼性は高くなってしまう。
本選択肢では「再検査法」について問われていますね。
「2時点の検査得点間の相関係数を用い、検査の安定性をみる」という本選択肢の再検査法に関する説明は適切なものであると考えられます。
よって、選択肢③が正しいと判断できます。
⑤ 検査得点の分散に占める真の得点の分散の割合が高いほど、検査結果の解釈が妥当になる。
古典的テスト理論では、測定値(検査得点のこと)を真値と誤差に分解し、信頼性を評価していきます。
真値(真の値)とは、簡単に言えば理論的な数値であり、実際にはいくら厳密に測定しても精度に限度があるので真の値を測定することはできません。
これは理論値なので「実際に存在すると仮定」しておく数字ということになります。
これに対して誤差とは、測定や理論的推定などで得られた近似値(測定値)と真の値(と考えられるもの)との差を指しています。
このように、測定値を真値と誤差の合計と見なした上で、古典的テスト理論では次の指標を使って信頼性を評価していきます。
- 測定の標準誤差:誤差の標準偏差で、これが小さいほど信頼性は高い。
- 信頼性指数:真値と測定値との相関係数で、大きいほど信頼性は高い。
- 信頼性係数:測定値の分散に占める真値の分散の割合で、これが大きいほど信頼性は高い。
- 信号=雑音比:真値の分散と誤差の分散との比で、大きいほど信頼性は高い。
- 一般化可能性係数:誤差が発生する要因は多様なので、分散分析の手法を適用して測定値の変動要因を分解し信頼性を評価する。大きいほど信頼性は高い。
本選択肢で問われているのは、上記の3に関する内容であると考えられますね。
このように、信頼性係数は「テストから得られる分散のうち、真の得点の分散の比率」という定義になっており、言い換えると「テストから得られる分散のうち、誤差の分散を除いた部分の比率」ということになります。
このことは言われてみれば当然のことで、測定値のバラつき具合(分散)に占める真値のバラつき具体(分散)が多いほど、信頼係数が高くなることがわかりますね。
ただし、実際に観測できるのは測定値の分散だけになり、真の得点の分散や誤差の分散は観測できないので、信頼性係数の推定を行っていくことになる(選択肢③の内容ですね)。
本選択肢の「検査得点の分散に占める真の得点の分散の割合が高いほど」という表現は信頼性係数を示すものであると考えられますが、この後には「検査結果の解釈が妥当になる」とあります。
「検査得点の分散に占める真の得点の分散の割合が高い」ということは信頼性という安定性・一貫性の指標に過ぎず、その「検査結果の解釈が妥当である」ことを意味しません。
以上より、選択肢⑤は誤りと判断できます。