問7はデータ解析を行う各分析法の特徴の把握を問う内容です。
あまり数字を持ち出して考えてもややこしいので、概念的に理解するということを念頭に置いて説明していきましょう。
問7 量的な説明変数によって1つの質的な基準変数を予測するための解析方法として、最も適切なものを1つ選べ。
①因子分析
②判別分析
③分散分析
④重回帰分析
⑤クラスター分析
まず基本用語を理解しておきましょう。
「独立変数」とは実験研究領域において研究者が操作する変数であり、「実験変数」や「処理」と呼ぶこともあるが、「従属変数」との対比で「独立変数」と呼ぶのが一般的です。
調査研究領域では「独立変数」のことを、「説明変数」とも呼びます。
また、従属変数とは実験研究領域において「独立変数」に依存して変化する変数のことを指します。
調査研究領域では「従属変数」のことを、「目的変数」「基準変数」とも呼びます。
本問の場合、量的な説明変数(独立変数)によって、1つの質的な基準変数(従属変数)を予測するための解析方法、を問われています。
大切なのは「量的な説明変数」「1つの質的な基準変数」「予測するため」というワードです。
独立変数のデータの種類、従属変数のデータの種類、何を使用しているのか、ということが明確になることで、使用できる分析手法が以下のように分かれます。
こちらを頭に入れておけば、本問のようなタイプの問題なら容易に解くことが可能です。
これらを踏まえて各選択肢を見ていきましょう。
解答のポイント
多変量解析の目的、尺度変数の種類、それらによって導かれる分析手法を把握していること。
選択肢の解説
①因子分析
ある国の国民性に関するイメージ調査で、あるアンケートを取ったが項目は以下のようなものだったとします。
- 時間を守りそうか
- メールをすぐに返しそうか
- 整理整頓が好きそうか
- 笑顔が多そうか
- 自分の意思を正確に伝えるのが得意か
- 相手の意図を正確に汲み取るのがうまいか
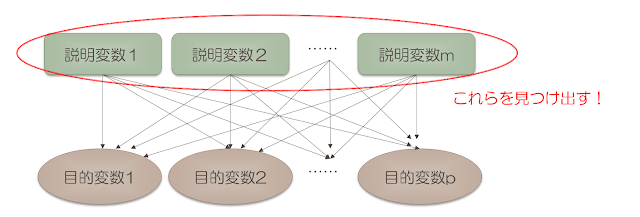
「きっと世の中に存在するに違いない「データの背後に潜む説明変数」を見つけ出す」分析手法とも言えますね。
上記のようなイメージ図になります。
因子分析は目に見えないプロセスの解明を目指す心理学の研究において、大変有用な手法です。
因子分析は量的変数に用い、その目的も背景にある因子を探ろうというものです。
以上より、選択肢①は誤りと判断できます。
②判別分析
⑤クラスター分析
判別分析は、目的変数が質的データ、説明変数が量的データとなる多変量解析です(説明変数が質的でもダミー変数を用いることができなくはないけど)。
判別分析は、どの群に属しているかが分かっている標本があるときに、まだ分類されていない標本がどちらの群に属するかを「予測」する手法のことを指します。
例えば…
- 各種の検査項目から、ある病気であるかないかを判別する。
- 各種アンケート結果から各々の消費者が、製品Aを選ぶか製品Bを選ぶかを予測する。
- 筆記試験、面接、作文、適性検査など多面的な試験項目からなる入社試験、入学試験において合格群と不合格群を判別する。
- 重金属の含有比から、出土品の金属がどの鉱山のものか推定する
- 甘味も苦みも強いチョコ
- 甘味が強いチョコ
- 苦みが強いチョコ
- 甘味も苦みも弱いチョコ
③分散分析
分散分析はフィッシャーによって1916年に開発されました。
フィッシャーは小麦の収穫量について、以下の3種類のバラツキを分けて考える必要があることに気づきました。
- 年度のバラツキ:植物生育を直接左右する天候の影響によるバラツキ
- 土壌の影響:土壌の持つ栄養が次第に減ってゆくことによるバラツキ
- ゆっくりとした変化:ランダムに発生する小さな変動によるバラツキ
分析の結果、「雨が多いと土地がやせる」という大きな流れ、つまり主効果を他の要素から分離することに成功したという経緯があります。
上記の分類をもっと統計的に言えば以下の通りです。
- データ全体のバラつき=全体平方和
- 平均値の違いで説明できるバラつき=群間平方和
- 平均値の違いでは説明できないバラつき=群内平方和
④重回帰分析
説明変数も基準変数も量的データであり「すべての変数の間で相関係数を算出できるとき」の分析には、重回帰分析を用いることができます。
このように、重回帰分析を使用できるのは、複数の説明変数によって1つの基準変数を説明しようというモデルにおいてです。
この時、説明変数相互の相関関係にも考慮し、その影響を取り除いて、各説明変数の純粋な影響を取り出すのが狙いになります。
上記のようなイメージです。
重回帰分析において、必ず理解しておかねばならないのが重相関係数と標準偏回帰係数についてです。
「重相関係数」とは、独立変数全体での影響の大きさを表します。
よって、重相関係数は1つのみです。
ただし、影響の向きを表すものではないので値は常に正の数になります。
一般にRで表され、普通の相関係数(r)は区別のために「単純相関係数」や「単相関係数」と呼ばれます。
「標準偏回帰係数」とは、他の変数の影響を取り除いた時の、独立変数の影響の大きさと向きを表します(βであらわされる)。