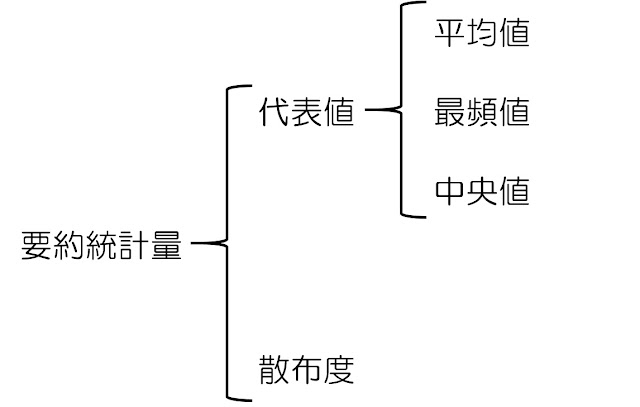
問6は順序尺度に関する理解を問う内容です。
まず求められるのは、少なくとも統計量を「代表値」と「散布度」に分類することです。
問6 順序尺度によるデータの散布度として、正しいものを1つ選べ。
① 中央値
② 平均値
③ 標準偏差
④ 不偏分散
⑤ 四分位偏差
重要なのは「散布度」という点になります。
散布度とは分布の広がりを示すものです。
各代表値(平均値、最頻値、中央値など)は、いわば分布の中心位置を示すものになりますが、中心位置が同じであっても、分布の様子が異なる場合もあります。
代表値だけでは分布の様子を的確に把握できないので、散布度を表す各基準が必要になってきます。
本問は、この散布度を表す基準について問うた内容と言えるでしょう。
解答のポイント
代表値と散布度の違いを把握できていること。
各尺度によって散布度を表す概念が異なることの把握。
選択肢の解説
①中央値
②平均値
データをデータのままで眺めていても、どういう傾向があるのか、特徴があるのかは分かりにくいものです。
ですから、それらのデータを1つの値に集約するという手法が取られ、その要約された値のことを要約統計量と呼びます。
そして、この要約統計量には「代表値」と「散布度」があります。
まず代表値とは、データの分布の様子を1つの値に代表させたもの、その分布の中心がどこに位置しているかを示すものです。
代表値には、平均値(全てのデータの値を足して度数で割ったもの)、最頻値(最も度数の多いデータの値)、中央値(データを大きさ順に並べて真ん中に位置する値)などがあります。
これらには、それぞれ用いられやすい状況があります。
一般的には平均値が使われることが多いのですが、1%の富裕層が99%の富を独占しているこんな世の中の年収についてみていく場合、1%の富裕層という「外れ値」があるので中央値の方が自分の現状を測るのに適している代表値ということになります(こういう外れ値によって値が引きずられない性質を「抵抗性」と呼び、中央値は抵抗性が高く、平均値は低いということになる)。
尺度の種類ごとに使われやすい代表値は定められています。
各尺度の特性、例、代表値については以下の表にまとめておきます。
ちなみに名義尺度の代表値が最頻値となっておりますが、正確には「名義尺度以上ならば最頻値が使える」ということと理解しておいてください。
より細かく言えば、以下のような表になるということです。
ちょっと余計なものも入っていて分かりづらいかもしれませんけど(別の講座で使ったものですから…)、このような感じだと理解しておきましょう。
散布度については他選択肢で細かく述べていきますが、大切なのは選択肢①および選択肢②は「散布度を示すものではなく、代表値の種類の一つである」という理解だと思います。
つまりは以下の図のような理解です。
このように代表値と散布度の違いを理解しておくことが大切になりますね。
以上より、選択肢①および選択肢②は誤りと判断できます。
③標準偏差
④不偏分散
⑤四分位偏差
冒頭で述べたとおり、散布度とは分布の広がりを示すものです。
各代表値(平均値、最頻値、中央値など)は、いわば分布の中心位置を示すものになりますが、中心位置が同じであっても、分布の様子が異なる場合もあります。
代表値だけでは分布の様子を的確に把握できないので、散布度を表す各基準が必要になってきます。
この散布度も代表値と同じく、尺度ごとに適用できるものが異なります。
上記の表に追加する形で記入しました。
このように散布度も尺度種によって用いられる(用いられやすい)ものがある程度定まっております。
ここでは本問で問われたものを説明していくことにしましょう。
まずは選択肢④の不偏分散についてです。
ちなみに「分散」と「不偏分散」という表現があります。
この違いは、分散は標本のみを考えた分散であるのに対して、不偏分散は標本の属する母集団全体について考えた分散の推定値を表しています。
分散は(データの値-平均)² を計算し、それらの合計をデータ数で割ったものです(不偏分散は(データ数-1)で割ったものになります)。
上記のように2乗の計算が入っているので、元の測定単位が変わってしまいます。
そこで、測定単位を戻すために平方根をつけると選択肢③の標準偏差になります。
不偏分散も標準偏差も、値が大きいほどバラつきが大きいことを示します。
細かい計算ルートを示せばその点は自明なことなのですが、そういうことが苦手な方は「数字が大きいとバラつきが大きいのだ」と覚えておくことです。
そして不偏分散もそれと連なる標準偏差も、計算の中で平均値という代表値を用いております。
よって、平均値を代表値として用いることが可能な間隔尺度以上でないと(つまりは間隔尺度と比例尺度)、不偏分散や標準偏差を散布度として用いることは困難であると言えますね。
さて、残った選択肢⑤の四分位偏差について説明していきます。
こちらは代表値として中央値を用いる場合に散布度の指標として用いられます(一般にはQという記号になる)。
四分位偏差を求める場合、まずデータを大きさの順に並べ、全体を4分の1ずつ分けます。
そして、値が小さい方から見た最初の分割点、つまりは下位25%の位置の値をQ₁、最後の3番目の分割点、つまりは上位25%の位置の値をQ₃とします(ちなみにQ₂は中央値:Meですね)。
その上で以下の公式によって計算されるのが四分位偏差になります(Q₃-Q₁の値は四分位範囲と呼びます)。
Q=(Q₃-Q₁)÷2
つまりは四分位範囲=中央値を挟んで全体の50%のデータの数の範囲、ということになります。
そして四分位偏差とは、全データの中央値周りの50% (Q₃ – Q₁) のバラつく具合を示す値になります。
すなわち、データ中に存在する極端に大きな値、または小さな値 (外れ値) の影響を受けにくい指標となるので、そういった状況下でデータのバラつき具合を算出したいときに採用されることになりますね(先の中央値の例として年収を挙げましたが、そういう時に用いるわけです)。
以上より、選択肢③および選択肢④は誤り、選択肢⑤が正しいと判断できます。