調査研究を行う際の研究対象者を抽出する方法に関する問題です。
研究法関連の書籍にはほぼ載っているような基本的な内容になりますが、意外と初出の内容でしたね。
問83 全対象者に一連の番号を付け、スタート番号を乱数によって決め、その後、必要な標本の大きさから求められた間隔で研究対象者を抽出する方法として、最も適切なものを1つ選べ。
① 系統抽出法
② 集落抽出法
③ 層化抽出法
④ 多段抽出法
⑤ 単純無作為抽出法
関連する過去問
なし
解答のポイント
調査研究を行う場合の対象者の選定方法を把握している。
選択肢の解説
⑤ 単純無作為抽出法
本問を考えていく上では、具体的な例を踏まえつつ解いていきましょう。
例えば、10000人から1000人を偏りなく選び出す方法として、10000人分のくじを作って、そこから1000人をくじ引きで選び出すというのが、最も単純な方法と言えます。
このように、母集団に含まれる個人に一連の番号を振り、その番号をくじと見なして、必要な数の標本をくじ引きによって選び出すのが単純無作為抽出法です。
この方法なら、くじ引きは選ぶ者の意思を排除することができ、標本が母集団をできるだけ正確に代表するようになっていることになります。
上記からもわかる通り、単純無作為抽出法は非常にシンプルな考え方に基づいていますが、その代わりに大変手間のかかる方法であるとも言えます。
特に、母集団の数が大きい場合には、一連の番号を振ること自体が困難となるため、研究デザインによっては使えない方法になります。
上記の通り、単純無作為抽出法とは「全対象者に一連の番号を振り、その番号をくじと見なして、必要な数の標本をくじ引きによって選び出す」という方法ですから、本問の「全対象者に一連の番号を付け、スタート番号を乱数によって決め、その後、必要な標本の大きさから求められた間隔で研究対象者を抽出する方法」とは合致しないことがわかります。
よって、選択肢⑤は不適切と判断できます。
① 系統抽出法
上記のような単純無作為抽出法に対し、誰もが等確率で選ばれるというルールを守りながら、抽出作業の簡易化を図った方法もあります。
まずは「ある調査の対象となる人物の全員の名前が名簿として手に入っているような状況」において、最初の抽出開始点を無作為に選んでいきます(例えば、さいころを転がすなどの方法ですね)。
その後、等間隔で標本を抽出し、規定の標本サイズが集まるまで標本抽出を続けていきます。
例えば、最初の抽出開始点を無作為に選んだ結果、名簿の7番目の人が最初の標本の要素として抽出されたとします。
標本抽出の間隔を「20人」として定めたとすると、最初の標本の要素が抽出された後は、20人おきに抽出を行っていきます(7番目、27番目、47番目…のように等間隔で標本の要素が抽出されることになる)。
このような方法を「系統抽出法(等間隔抽出法)」と呼び、単純無作為抽出法よりも手間がかからない方法と言えますが、リストの並び順に周期性がある場合には標本に偏りが生じる可能性が出てきてしまいます。

上記(こちらのサイトから引用)を踏まえれば、系統抽出法は「全対象者に一連の番号を付け、スタート番号を乱数によって決め、その後、必要な標本の大きさから求められた間隔で研究対象者を抽出する方法」であると言えますね。
よって、選択肢①が適切と判断できます。
② 集落抽出法
集落抽出法は「クラスター抽出法」とも呼ばれ、①母集団を小集団である「クラスター(集落)」に分け、②分けられたクラスターの中から、いくつかのクラスターを無作為抽出し、③それぞれのクラスターにおいて全数調査を行う、という方法になります。
クラスターの情報さえあれば抽出することができるので、時間や手間を節約できる反面、同じクラスターに属する調査対象は似た性質を持ちやすいため、標本に偏りが生じる可能性があります。
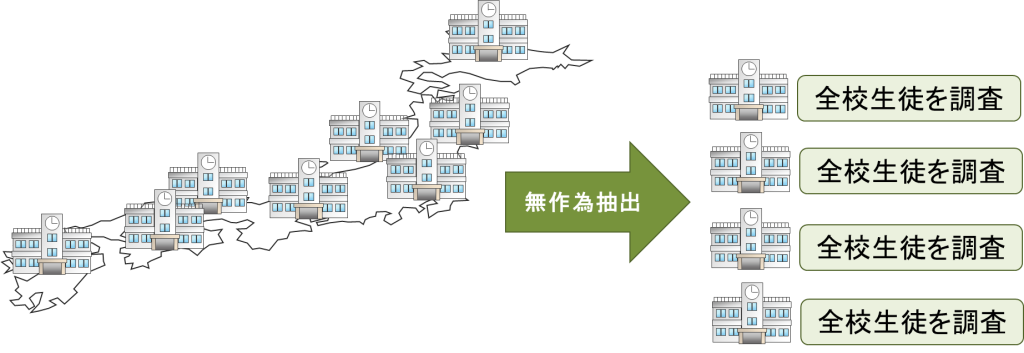
このように、集落抽出法とは「母集団を小集団である「クラスター(集落)」に分け、分けられたクラスターの中からいくつかのクラスターを無作為抽出し、それぞれのクラスターにおいて全数調査を行うという方法」になり、本問の「全対象者に一連の番号を付け、スタート番号を乱数によって決め、その後、必要な標本の大きさから求められた間隔で研究対象者を抽出する方法」とは合致しないことがわかります。
よって、選択肢②は不適切と判断できます。
③ 層化抽出法
母集団から標本を抽出するときに、まず、母集団全体をいくつかのグループ(これを層と呼ぶ)に分けます(これを層化と呼びます)。
分けられたそれぞれのグループから必要な数の標本を無作為に抽出していく方法を指して「層化抽出法」と呼びます。
母集団全体を層に分けるときに、すなわち、層化する際に、層間に比べて層内がなるべく等質になるようにグループ分けを行うことが標本の精度を上げるために重要となります。
例えば、事前に人口規模、地域特性、産業構成比などの特性を考慮して母集団をいくつかの層に分け、各層から層の大きさに比例して無作為抽出を行う場合などを「層化抽出法」と呼ぶわけですね。
こちらのサイトがわかりやすかったので、画像を引用します。
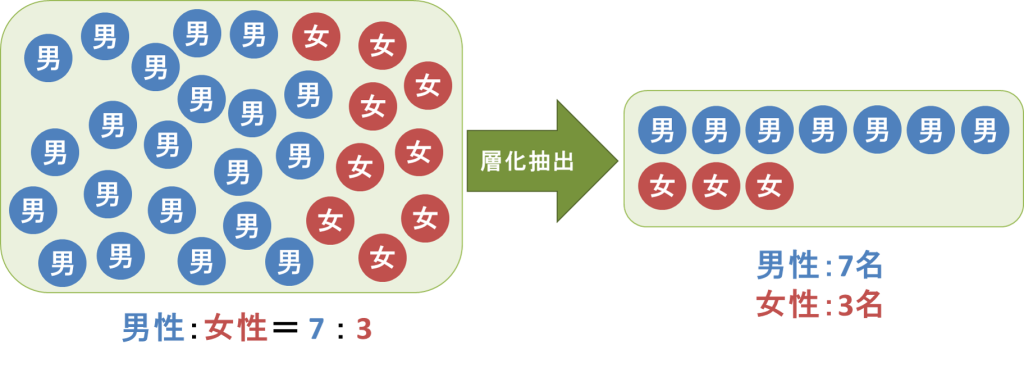
以上のように、層化抽出法とは「いくつかの部分母集団(層化)に分割し、各部分母集団から標本を抽出する方法」であり、本問の「全対象者に一連の番号を付け、スタート番号を乱数によって決め、その後、必要な標本の大きさから求められた間隔で研究対象者を抽出する方法」とは合致しないことがわかります。
よって、選択肢③は不適切と判断できます。
④ 多段抽出法
標本調査において、まず母集団を分割した群のいくつかを抽出し、次に抽出された各群の中で調査対象となる個体を抽出する方法を「2段抽出法」と呼びます。
例えば、全国からまず都道府県をいくつか選び、次にそれら各県内の高校を抽出し、さらに各高校から生徒を抽出するというように抽出の段階を増やすと、一般に「多段抽出法」と呼ばれる方法になります。
調査対象となる個体のリスト作成や訪問調査におけるコスト・労力が抑えられる一方で、誤差が大きくなりやすいという特徴をもちます。
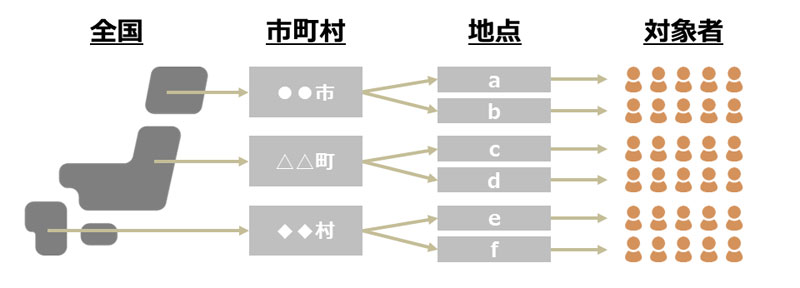
上記のように、標本の抽出を複数の段階で行う方法を多段抽出法といいます(こちらのサイトがわかりやすかったので引用します)。
図のように、全国の世帯を対象として調査を行う場合、まず全国からいくつかの市町村を無作為に抽出し(第一段)、次にその市町村内で地点を無作為に抽出し(第二段)、さらにその中で世帯を無作為に抽出します(第三段)。
多段抽出法の最大のメリットは、対象者を訪問面接する際に、対象者が地点ごとにまとまっているため、調査員の移動距離が少なく、効率的に調査ができることです。
上記の通り、本問の「全対象者に一連の番号を付け、スタート番号を乱数によって決め、その後、必要な標本の大きさから求められた間隔で研究対象者を抽出する方法」と多段抽出法は合致しないことがわかります。
よって、選択肢④は不適切と判断できます。