ヒトの聴覚についての問題ですが、実際には音響心理学などの分野の知識も求められており、なかなかの難問です。
でも耳の聞こえについては臨床場面で時々出てくる主訴ですし、「根っこの部分から知っている」という事実が自分の臨床を支えてくれることもありますから理解に努めましょう。
問83 ヒトの聴覚について、正しいものを1つ選べ。
① 蝸牛にある聴覚受容器は、双極細胞と呼ばれる。
② 音源定位には、両耳間時間差と両耳間強度差が用いられる。
③ ピッチ知覚の場所説は、高周波音の知覚の説明が困難である。
④ 聴覚感度は、可聴域内で周波数が高くなるほど単調に減少する。
⑤ 主観的な音の大きさであるラウドネスの単位は、デシベルである。
解答のポイント
ヒトの聴覚に関する生理学、音響心理学的な理解がある。
選択肢の解説
① 蝸牛にある聴覚受容器は、双極細胞と呼ばれる。
内耳は聴覚器(蝸牛)と平衡器(前庭と半規管)から構成されており、聴覚受容器官は内耳の蝸牛ということになります。
蝸牛はカタツムリ(漢字だと蝸牛ですね)の殻のような形をした器官であり、内耳の中では前内側に位置します。
中耳から伝わった機械信号である音波を電気信号に変換し蝸牛神経から脳へ伝える役割を担っています(これが「音を感知する」ということ)。
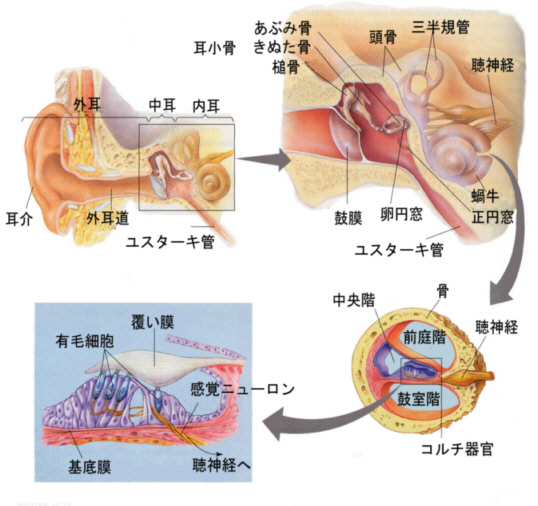
蝸牛の基底部から頂部に至るらせん状の構造を全体として形作っているのがコルチ器官です。
コルチ器官は聴覚の受容器細胞である有毛細胞と、複数の支持細胞で構成されています。
音の振動は蝸牛の中のリンパ液を通り、その振動によって基底膜が歪み、蓋膜とのずれが生じて有毛細胞の感覚毛が曲がります。
これによって有毛細胞が脱分極し、蝸牛神経に活動電位を発生させ、脳に音が伝えられるという仕組みです。
聴覚の伝導路としては、以下の通りになります。
- 蝸牛に伝えられた音の振動は、有毛細胞で電気信号に変換される。
- らせん神経節に細胞体を持つ蝸牛神経によって、蝸牛神経核に伝えられる。
- その後、対側または同側の上オリーブ核を経て、外側毛帯を通り、両側の中脳下丘に入る。
- 下丘でも左右の繊維連絡があり、視床の内側膝状体に入り、聴放線を通って、最終的に側頭葉聴覚野に至る。
なお、聴覚の伝導路は複雑で、この他にも多くの側副経路があります。
このように、聴覚受容器は有毛細胞になるので、本選択肢の内容は誤りとなります。
では、本選択肢の「双極細胞」がなにかも理解しておきましょう。
こちらは網膜の構造に出てきますので、視覚に関連する細胞です。
網膜には3つの細胞層、すなわち、視細胞層(桿体細胞、錐体細胞に分類される)、内顆粒層(双極細胞層)、神経節細胞層があります。
視覚情報の主な経路として、視細胞→双極細胞→神経節細胞と伝えられます。
内顆粒層には、視細胞から直接シナプス連絡を受ける双極細胞、水平細胞の2つの二次ニューロンの他に、双極細胞から入力を受けるアマクリン細胞(無軸索細胞)の細胞体が存在します。
以上より、選択肢①は誤りと判断できます。
② 音源定位には、両耳間時間差と両耳間強度差が用いられる。
ヒトや動物の行動にとって重要な音の情報の一つは、音の発生する源に関する情報です。
餌を捕えるために、あるいは危険を避けるために(そもそも聴覚は危険察知が第一の機能)、そしてコミュニケーションのために、ヒトにとっても動物にとっても、音の発生する方向を正しく認識し発生源を識別できることが大切です。
こうした音の発生する方向を正しく認識し発生源を識別できることを「音源定位」と呼びます。
正面を外れた音源から生ずる音には、左右の耳に到達する時間、および強度の違いに加えて、各周波数成分の総体強度や、頭あるいは耳介を動かすことによる変化の程度に違いが生じます。
ヒトはそうした音の情報を総合して音源定位を特定しているとされています。
音源定位の研究においては、左右両耳間での音波の到達する「時間差」および「強度差」の識別能力の解析が集中的に行われています。
ヒトも含めた多くの哺乳類においては一般に高周波音では「両耳強度差」を、低周波音では「両耳時間差」を使っていると考えられています。
高周波音は頭部を回折しにくい為に、より大きな「両耳強度差」を生じ易く、一方、低周波数音は周期が長いために「両耳時間差」を検出する際の音の周期性に由来するあいまいさ(位相多義性)が生じにくいとされており、合理的な理路と言えます。
ヒトも含めた多くの哺乳類や鳥類においては、主に「両耳時間差」および「両耳強度差」の情報を検出することで水平方向の音源定位を行っている。
他に音源定位に関与する聴覚情報としては、単耳性情報として各周波数成分の相対強度や耳介による変化の程度等が上げられ、特に哺乳類においては上下方向や前後方向の識別に重要になります。
ヒトも含めた動物はそうした様々な音の情報を統合することで音源の位置を特定しているわけです。
事実、純音(1つの周波数の正弦波から成る純粋な音。音色には特徴がなく、音の高さは一定であり、単調な感じがする)の場合になると、こうした音源定位の機能がうまく働きにくいため、音源定位が非常に難しくなります。
以上より、音源定位には両耳間時間差と両耳間強度差が用いられていることがわかりますね。
よって、選択肢②が正しいと判断できます。
③ ピッチ知覚の場所説は、高周波音の知覚の説明が困難である。
音のピッチとは音の高さ(pitch)のことで、音の大きさ(loudness)、音色(timbre)と並んで音の三属性の一つとされており、ピッチに対応する物理量のことを「基本周波数」と言います。
聴覚理論の関心の一つとして、聴覚刺激の周波数の違いをどのように聴覚系が取り扱うかというテーマがあり、周波数の違いは多くの場合、主観的にはピッチの違いに対応するため、聴覚説が説明する知覚現象の核にはピッチ知覚がおかれました。
要するに「人間が聴覚刺激の周波数の違いをどのように認識しているのか?」という点が音響心理学においては重要なテーマとなってきた歴史があるということですが、これを説明する有力な説として「場所説」と「時間説」が挙げられています。
これらの違いについて、順を追って説明していきましょう。
まず「場所説」とは、Helmholtz(1857)が唱えた説であり、入力信号の周波数によって、基底膜の反応位置が異なり(基底膜上で周波数分析を行っている)、さらに聴神経においても周波数の部位的構造がみられる(周波数局在性)ことから、基底膜上のどの有毛細胞が興奮するかによって音の高さが知覚されている、とする説です。
つまり、音の高さ(ピッチ)の知覚は、その音が共鳴する内耳の基底膜上の場所によって決まるという考え方ですね。
音のピッチによって基底膜上の有毛細胞がプルプルと反応する場所が違うので、その場所の違いによって音のピッチの違いを認識しているということです。
ある音のピッチは、その音の波形に含まれる周波数成分と強い関係があります。
単独のサイン波で表される音(純音)ならば、当然のことながら、その周波数がピッチを決めることになります。
一方で、複数のサイン波の合成でできた複合音であれば、通常は最も低い周波数(基本周波数)がピッチを決めことになります。
我々が歌を歌うときや楽器を演奏する時に、周波数成分の構成が異なる色々な音(楽器音や歌声)のピッチを合わせることができるのは、自然とそれぞれの基本周波数を合わせているからです。
こうしたピッチを捉えることができるのは、基底膜上のどの「場所」にある有毛細胞が興奮するかによって音の高さが知覚されているとするのが「場所説」なわけですが、この考え方にも矛盾があるとされており、その代表的なものがミッシング・ファンダメンタル現象です。
周期的な波形をフーリエ解析した場合に、その基本周波数の振幅がゼロになる場合を「ミッシング・ファンダメンタル」と呼びます(要は、基本周波数が欠落している音のこと)。
なお、フーリエ解析とは「周期的な波として捉えられる現象は全て単純な正弦波(正弦関数として観測可能な周期的変化を示す波動のこと)の重ね合わせで表現することができる」という前提の下、数学的テクニックを駆使し積分などの計算を行うことで振動している何か(音、電圧、画像データなど)を解析する手法です。
ミッシング・ファンダメンタル現象とは、複合音の基本周波数成分を取り除いた場合でも、その基本周波数成分と同じピッチが知覚される現象のことです。
つまり、基本周波数を欠いた倍音列を聴くと、存在しないはずの基本周波数のピッチが知覚されることになり、例えば、780Hz、1040Hz、1300Hzという周波数成分を持つ複合音を聴くと、基本周波数としてこれらの最大公約数である260Hzのピッチが知覚されることになります。
このミッシング・ファンダメンタル現象は、ピッチの「場所説」では説明ができません。
先述の通り、複数のサイン波の合成でできた複合音であれば、通常は最も低い周波数(基本周波数)がピッチを決めことになるはずです。
となれば、ミッシング・ファンダメンタルの状態で知覚されるピッチは基本周波数に対応したものではなく、存在する最低の周波数のものとならなければならないはずですが、そうはならずミッシング・ファンダメンタル現象が生じています。
つまり、ピッチの「場所説」では、低周波音(基本周波数)の知覚の説明が難しくなるのです(ここが本選択肢の正誤判断になりますね)。
この現象を説明するために、Rutherford(1886)の「時間説」が導入されました。
これは基本周波数が除去された複合音でも、周期は基本波と同じ周期を持ちますので、この周期と同期して神経が発火すれば基本周期が検出できる、すなわち、時間情報から音のピッチが知覚可能という考え方です。
つまり「時間説」では、音に対して同じ振幅の位相をキャッチしていき、その時間的な繰り返しパターンと、神経発火の時間パターンが関係している、と考えるわけです。
ただし、位相固定は、4000Hz以上で消失しますので、その音域では基底膜上の場所的手がかりに頼ることになり、ピッチ認識は不正確になります。
このように、高調波間の位相効果が観察されない、高調波の次数にも上限があるなどが明らかにされ、時間説のみではすべての現象を説明できなくなりました(つまり、本選択肢の内容は「場所説」ではなく「時間説」について述べたものと言えますね)。
その他にも、時間説が唱えられた当時は神経発火の大きさが一律であるという生理学的な発見がなされておらず、その発見によって説に矛盾が生じる等、その信ぴょう性を揺るがす事実も示されるようになってきました。
なお、近年の聴覚説は、時間説と場所説の折衷となっていることが多く、すなわち、大雑把な音の高さの感覚を与えるのは場所説を、詳細な高さの感覚は時間説で説明されるようになっています。
すなわち、本選択肢の「高周波音の知覚の説明が困難である」というのは「場所説」ではなく「時間説」の説明であること、実際の「場所説」においては「低周波音(基本周波数)の知覚の説明が困難である」ことがわかりますね。
以上より、選択肢③は不適切と判断できます。
④ 聴覚感度は、可聴域内で周波数が高くなるほど単調に減少する。
⑤ 主観的な音の大きさであるラウドネスの単位は、デシベルである。
人間の耳に聞こえる音の大きさは、どんな周波数でも一定ではなく、周波数によって耳に聞こえる音の大きさは変わります。
人間の可聴範囲は周波数で20~20,000Hz(約10オクターブ)にわたり、音圧レベルでほぼ0~120dB(106倍)の範囲となり、周波数的にも音の強さにおいても広い範囲の音を聞き取ることができるとされています。
可聴領域の中でも、人間の耳が聞きとりやすい感度のいい(つまり大きく聞こえる)周波数帯があり、それが2,000Hz~4,000Hzの高さの音とされており、この周波数には赤ちゃんの泣き声や、女性の悲鳴、家電製品の警告アラームなどの音があります。
人の耳は周波数によって聴こえる音の大きさ(耳の感度)が違うのですが、この聴こえ方をグラフにしたものが等ラウドネス曲線というものです。
ラウドネスとは、音の大きいから小さいまでの尺度で測れる心理量のことを指し、その範囲は絶対閾から刺激頂までになります。
絶対閾以下の音圧だと感覚は生じませんし、逆に刺激頂を超えると痛覚として感じることになります。
音の大きさの知覚というのは、周波数によって音圧は同じでも感じる大きさは異なります。
逆に言えば、同じ大きさに感じるように各周波数で音圧をコントロールしてもらえば、各周波数では、異なる音圧になるということです。
その測定結果を表したのが等ラウドネス曲線になります。
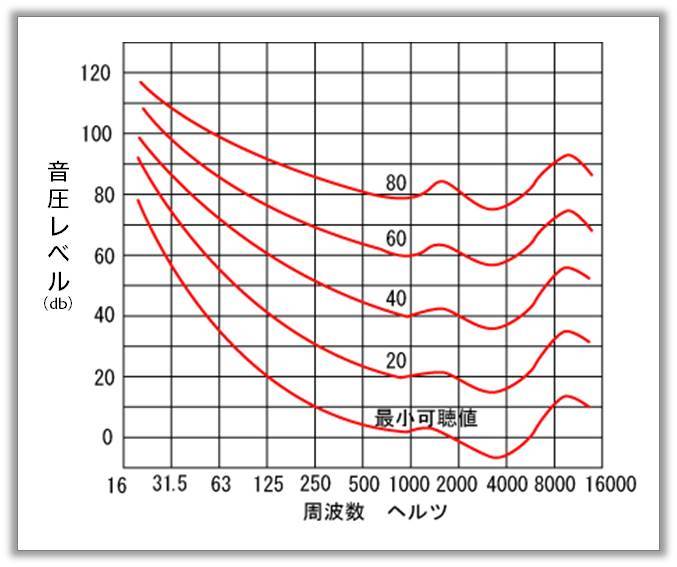
上述の通り、2,000Hz~4,000Hzでは最もよく聞こえるようになっていますが、周波数が低いと聞き取りにくくなっており、また、周波数も一定以上になると聞こえにくくなっています。
上の図ではちょっと高周波数に関してはわかりにくいので、以下の図を見てください。
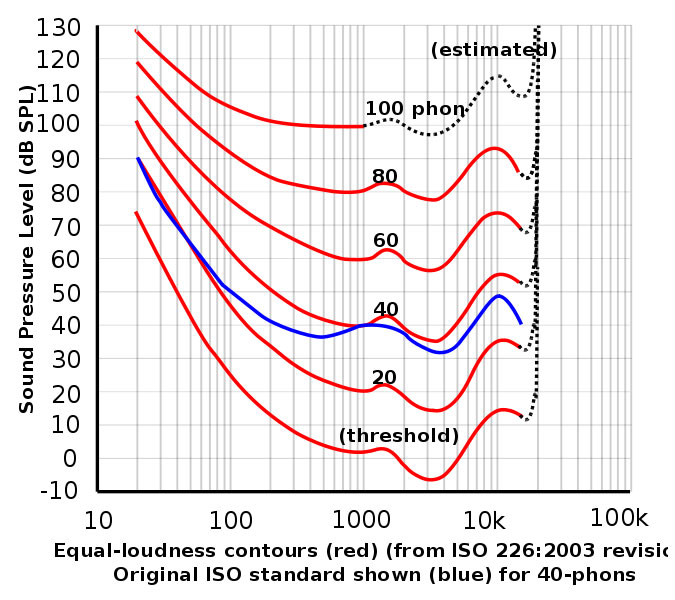
このように、2,000Hz~4,000Hzを頂点として、低周波数および高周波数(大体5,000Hz以上)で人間の耳の感度が悪くなっていくのがわかりますね。
この点が、選択肢④で示されている「聴覚感度は、可聴域内で周波数が高くなるほど単調に減少する」が誤りであるという理由になります。
さて、上の図の縦軸横軸になっている周波数と音圧についてまずは理解しておきましょう。
周波数とは、音の波が1秒間に振動する回数であり、単位は「Hz:ヘルツ」で表します。
周波数の違いは、そのまま音の高低となり、周波数の低い(振動回数の少ない)音は低い音、周波数の高い(振動回数の多い)音は高い音となります。
そして、音は主に「空気の圧力」が変化する現象ですので、その強さを通常は「音圧」で表し、この単位は「Pa:パスカル」です(台風のときのアレ。hPaのヘクトは100という意味)。
「音圧」を表す「Pa」ですが、人が何とか聞こえる最小の音圧を「20マイクロパスカル(μPa)」と定め、音圧を比較する場合はこれを基準としてどれくらい大きいかを「dB:デシベル」という単位で表現します。
音圧に関しては、非常に単純化して言うならば「音の大きさ」と思っておいて良いと思います。
図では、赤い曲線が数本うねうね+数字が表示されていますが、この数字は「人の耳に聞こえる音の大きさ」=「ラウドネス(音の聴覚的な強さ)」を示す曲線で、単位は「phon:ホーン(ホン)」で表されます。
例えば、ちょうど1,000Hzのところで左の音圧レベルを見ると40dBになっていますから「1,000Hzの周波数で40dBの音圧レベルの音は、人の耳で40ホンの大きさに聴こえる」ということを意味しています。
この「40phonの大きさに聴こえる」ということが重要で、等ラウドネス曲線とは「人の耳で同じ音の大きさに聴こえる周波数と音圧レベルの関係を表したグラフ」ということになるわけです。
そして等ラウドネス曲線を見ればわかる通り「同じ音圧レベルであっても周波数が違うと同じ大きさに聴こえない」ということになりますね。
この等ラウドネス曲線は、例えば、家電製品の音が聞こえやすい周波数になるよう設計するとか、音楽制作において、全体の音量バランスを取り、違う高さの音が等しく聴こえるための基準にするなどに活用されています。
以上より、人間の可聴域では2,000Hz~4,000Hzを頂点として、低周波数(大体100Hz以下)および高周波数(大体5,000Hz以上)になると聞き取りにくくなることが示されています。
また、それを示す等ラウドネス曲線のラウドネスの単位はphonとなります。
よって、選択肢④および選択肢⑤は誤りと判断できます。