統計的仮説検定に関する問題です。
問われていることは各統計手法での定石になりますが、いかんせん言葉が難しいので理解に時間がかかります。
まず「何を言っているのか」を理解することが大切ですね。
問7 統計的仮説検定の説明として、正しいものを1つ選べ。
① t検定では、自由度が大きいほど、帰無仮説の上側確率に基づく棄却の限界値は小さい。
② 2つの条件の平均に有意な差が認められない場合、それらの平均には差がないといえる。
③ K. Pearsonの相関係数が0.1%水準で有意であった場合、2つの変数間に強い相関があるといえる。
④ 対応のない2群のt検定では、各群の標準偏差が大きいほど、有意な差があるという結果が生じやすい。
⑤ K. Pearsonの相関係数の有意性検定では、サンプルサイズが小さいほど、帰無仮説の上側確率に基づく棄却の限界値は小さい。
解答のポイント
各統計手法の有意になりやすい状況、なりにくい状況を理解していること。
選択肢の解説
① t検定では、自由度が大きいほど、帰無仮説の上側確率に基づく棄却の限界値は小さい。
一つひとつの用語を理解すればそれほど難しい内容ではありません。
まず最初は「t検定」とは何か簡単に理解しておきましょう。
t検定は、2つの標本の平均値の差の検定に利用されるt検定を指すことが一般的ですし、本選択肢でもそのように捉えて問題ありません。
ちなみに、t検定の従属変数は、間隔尺度か比例尺度(要は数量化されている量的変数)になります。
2つの平均値の差を比べるわけですから、標本Aと標本Bの平均値が示され、その差がどのくらいかを数値化していきます。
この数値化する時に用いるのが「t値」というもので、これは「t値=(標本平均の差)/(標本平均の差の標準誤差)」で示されます。
詳しい計算の仕方はともかく、「2つの平均値の差を調べるために「t値」という、2つの標本の差を表す値を計算するのだ」くらいは覚えておきましょう。
そしてt検定では、この「t値」は、「自由度」の「t分布」に従うものなのです。
これはどういう意味かを説明していきます。
t検定において自由度は「(標本Aの数-1)+(標本Bの数-1)」によって示されます。
つまり、t検定においては「自由度が大きい=データの個数が多い」「自由度が小さい=データの個数が少ない」と覚えておけば良いです。
例えば、標本数がAB両方とも5なら、「(5-1)+(5-1)=8」となりますね。
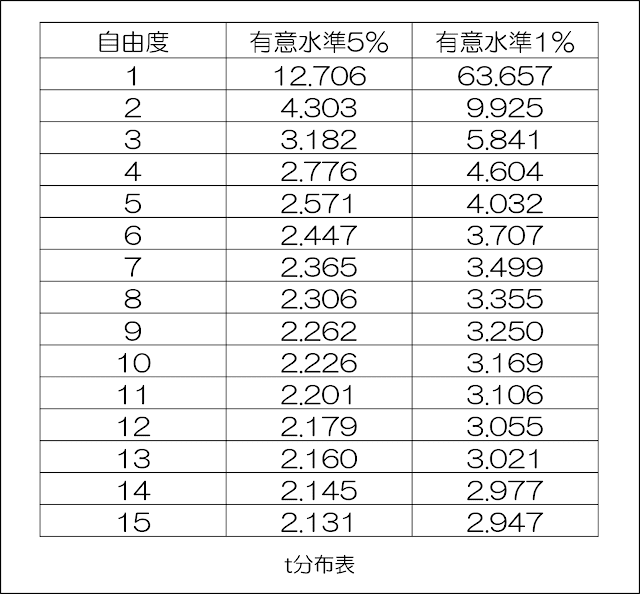
こうして示された自由度を以下のt分布表で見ていきます。
例えば、自由度が8なら、有意水準5%は「2.306」となります。
そして、先述した「t値」という標本Aと標本Bの平均値の差を数値化した指標が、この分布表の数字を超えていたならば「帰無仮説を棄却できる」「有意な差が認められる」となるわけです。
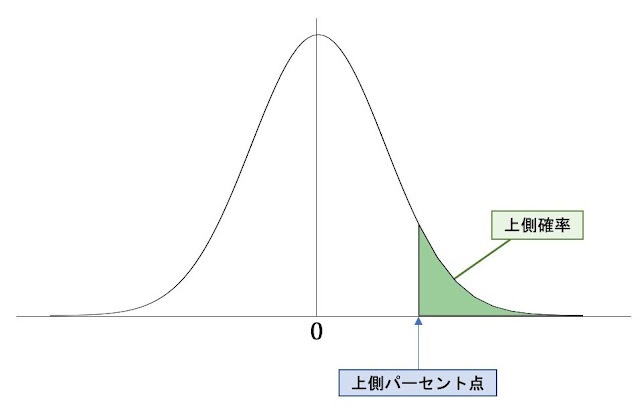
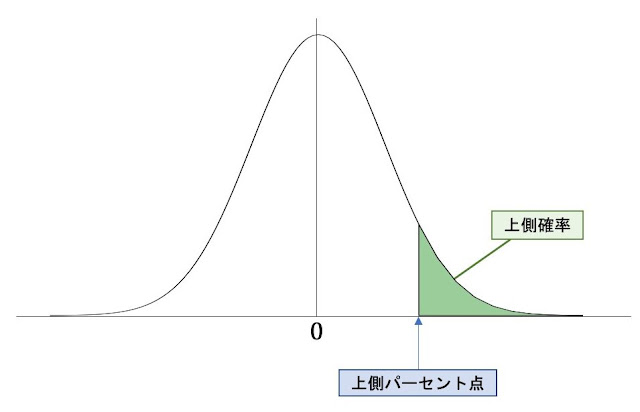
これを図で表すと以下のようになります。
上記の「上側パーセント点」というのが、有意水準5%(もしくは1%)を示す値の位置ということになり、示された「t値」がこの上側パーセント点よりも右側の「上側確率」という部分にかかっていれば「帰無仮説を棄却できる」「有意な差が認められる」ということになるのです(上側確率の緑色になっている部分を「棄却域」と呼びます)。
さて、ここまでを踏まえて本選択肢の「t検定では、自由度が大きいほど、帰無仮説の上側確率に基づく棄却の限界値は小さい」ということの意味を説明していきます。
上記のt分布表を見てもらえればわかると思いますが、自由度が大きくなるほどに有意水準が5%であれ1%であれ、数字がどんどん小さくなっているのがわかりますね。
これは上の図で言えば「上側パーセント点」が、どんどん左側に移動していっているということになり、帰無仮説が棄却されるポイント(上側パーセント点)が中心の「0」に近づいていくことになります。
そして、この「上側パーセント点」が左に寄っていくということ(有意水準の数字がどんどん小さくなっていくこと)が、本選択肢の「上側確率に基づく棄却の限界値は小さい」ということを指すのです。
このように見ると、本選択肢の「t検定では、自由度が大きいほど、帰無仮説の上側確率に基づく棄却の限界値は小さい」というのは正しい内容であることがわかります。
以上より、選択肢①は正しいと判断できます。
② 2つの条件の平均に有意な差が認められない場合、それらの平均には差がないといえる。
こちらは統計に関する基本的な考え方が問われています。
統計では、何かしらの要因を設定し(独立変数)、それ以外の要因(剰余変数)が作用しないように統制します。
そして、その研究デザインにあった統計手法を用いて「その数値の偏りが、何も要因が設定されていない状態であったら、どのくらいの確率で生じるのか」を出します。
例えば、「超能力でさいころの目を操作できる」という研究を行うため、1000回さいころを投げて、偶数が出た回数と奇数が出た回数を記録したとします。
この場合、超能力が研究者が設定した要因ということになりますね(そして、それ以外のさいころの目に影響が出そうな要因は均しておきます。つまり統制する)。
この結果、奇数が542回、偶数が458回出たとします。
そして計算すると、1000回のうち、偶然542回以上奇数の目が出る確率は「1%以下」ということがわかりました(実際にそうですよ)。
- 何も要因が設定されていない、自然なままの状態だと、この数字の偏りは1%以下の確率でしか生じない。
- そこまで低い確率でしか生じない数字が出てきたということは、研究者が設定した要因がこの偏りを生み出したのではないか。
さて、ここからが本題です。
上記の例の「1%」という数字を統計では「有意水準」や「危険率」と表現します(ここでは1%を例にとっていますが、5%、0.1%等状況によって様々な有意水準を設定します)。
なぜ「危険率」という物騒な表現をするか、理解しておくことが重要です。
それは「1%水準で有意な差が見られたという結果が得られた場合であっても、もしかしたら研究者が設定した要因は何も作用してなくて、たまたま「僅か1%」が出ただけ」という危険があるということです(1%水準であれば、なにも要因を設定してなくても、その数字の偏りは100回に1回は出るわけですからね)。
つまり、1%以下の確率で「本当は有意な差がないのに、有意な差があると間違えちゃう危険」があるということを意味するために「危険率」と表現するわけですね。
このような「本当は影響が「ないのにある」と誤ってしまうこと」を「第1種の過誤」(Type1Error:偽陽性;α)といいます。
これに対して、研究者の設定した要因が、本当は影響を与える力を持っていたのに、それがうまく働かないということもあり得ます。
そのような場合は「本当は影響が「あるのにない」と誤ってしまうこと」であり、これを「第2種の過誤」(Type2Error:偽陰性;β)と呼びます。
さて、これらを踏まえて、本選択肢の内容を見ていきましょう。
「2つの条件の平均に有意な差が認められない場合、それらの平均には差がないといえる」という表記ですが、まず「2つの条件の平均に」という箇所に関してはあまり気にしなくてよいです。
重要なのは「有意な差が認められない場合」=「それらの平均には差がない」という方程式が成り立つか否かの判断になります。
統計の基本的な考え方として、「有意な差が認められない」は「差は無かった」とか「関連は認められなかった」という解釈は許されません。
「有意な差が認められない」とは、言い直すと「仮説は棄却されなかった」ということであり、肯定も否定もされない中途半端な状態を意味しています。
その理由の代表的なものが、上記の「第2種の過誤」の存在です。
つまり、本当は影響があったかもしれないのに、それが発揮されなかっただけという可能性もあります。
また、1%水準で設定していた研究デザインであった場合、例えば、5%水準であれば有意な差が見られる結果になったかもしれません。
ですから、有意な差が認められないという結果が得られたとしても、どの程度の水準であったのかを見直し、場合によっては実験デザインを工夫することで(例えば、見落としていた剰余変数を統制するなど)、より鮮明に設定した要因の効果が出るようになるかもしれません。
このように、「2つの条件の平均に有意な差が認められない場合」≠「それらの平均には差がない」ということになるわけです。
以上より、選択肢②は誤りと判断できます。
なお、「2つの条件の平均に有意な差が認められた」という状況においては、「それらの平均には差がある」「関連が認められる」という解釈が許されます。
「有意な差は認められない」ときには白黒はっきりできないのに、「有意な差が認められた」ときは、ずいぶんとくっきりできています。
これはなぜか?
統計的仮説検定では、まず「帰無仮説」を立てます。
これは読んで字の如く「無に帰す仮説」です。
上記の超能力の研究で言えば、「超能力がある」ことを証明するために、「超能力は無い」という仮説を立て(これが帰無仮説)、これを棄却することで、やや遠回りをする形で「超能力はある」と証明するのです。
なぜこんな面倒くさいことをするのでしょうか?
超能力を例に、仮に「超能力がある」という仮説を帰無仮説にとってみるとわかりやすいです。
すると、「超能力がある」ということは、サイコロを振って100%奇数の目を出せる能力から、90%、80%、70%…などといろいろな数、厳密にいえば無限大の数の能力が含まれることになります。
これだと各々の場合について検証が必要となり、事実上この検証を実践することは不可能と言えます。
これに対して「超能力がない」という仮説は内容が一つであり、とても明快で曖昧性が排除されたものであることがわかりますね。
この「超能力がない」という帰無仮説を、棄却する(文字通り無に帰す)ことによって、「超能力がないという仮説が退けられたのだから、超能力が存在すると証明された」ということになるわけです。
このことを本選択肢の内容に沿って説明していきます。
「2つの条件の平均」を考えるときに、まずは「2つの条件の平均には差がない」という仮説を立てます(これが帰無仮説)。
そして、平均の差を統計にかけた結果、帰無仮説が棄却された場合、差がないという仮説が棄却された=差がある、という判断をするわけです。
こうなると、「それらの平均には差がある」「関連が認められる」ということを明確に述べることが許されるということになるわけですね。
このことを知っておけば、本選択肢の内容は「帰無仮説が棄却されなかった状況」を表現したものであることがわかるはずですね。
そして「帰無仮説が棄却されなかった」という状況は、それ以上でもそれ以下でもなく「白黒つけられないねー」ということが示されただけということになるわけです。
③ K. Pearsonの相関係数が0.1%水準で有意であった場合、2つの変数間に強い相関があるといえる。
こちらはちょっとしたひっかけ問題ですね。
「有意水準」と「相関係数」に関する理解が重要になってくる内容です。
まず、変数間の相関の強弱を見るのは「相関係数」です。
相関係数は、-1.0~1.0の間で表現されます。
0が無相関ということであり、負の数字であれば逆相関(片方が上がると、もう片方が下がる)ということを指します。
相関係数は「r」で表現され、その数字によって以下のように捉えます。
このように相関の強さは、相関係数の数値で見ていくことになります。
これに対して「有意水準」は何を意味するのでしょうか。
選択肢②でも示した通り、有意水準は「その数値の偏りは滅多に起こらないものですよ」ということの基準に過ぎません。
普通は、強い相関があるなら「有意な差がある」ということとイコールになると考えてしまうのではないかと思いますが、これはイコール関係ではありません。
例えば、1000という標本があれば、相関係数(r)は「0.062」という極めて小さな相関係数であっても「有意な差がある」となってしまいます(この点は選択肢⑤でも詳しく述べていきましょう)。
これは、統計的検定には「データ数という研究者が任意に決めることができる要因によって結果が左右される」という根本的な問題があるためです。
その仕組みを理解するのは難しいとしても、とにかく「標本が多いと僅かな相関関係でも有意になる」というのは、相関の代表的な陥穽であることは覚えておいて損はないと思います。
このように、「有意水準」と「相関の強さ」は比例しないということになりますから、本選択肢の表現は誤りと言えます。
そして、相関の強さを見たいのであれば、本選択肢には示されていない「相関係数」を見る必要があるわけですね。
以上より、選択肢③は誤りと判断できます。
④ 対応のない2群のt検定では、各群の標準偏差が大きいほど、有意な差があるという結果が生じやすい。
まずは対応の有無について理解しておきましょう。
対応が有るとは「測定対象は同じで、条件を変えて測定したデータ」のことです。
具体的には、ある子ども10人の血圧を測り、その1か月後に同じ10人の血圧を測って、その平均値を比べる場合などは「対応あり」になります。
これに対して、対応が無いとは「異なる測定対象から得られたデータ同士を比べる場合」のことを指します。
具体的には、老人の血圧の平均値と、子どもの血圧の平均値を比べる場合などは「対応なし」になりますね。
対応の有無によって、測定方法が変わってきます。
なぜなら、両群とも平均値の差を検定していることは同じであっても、対応のあるt検定は2群間に現れた差のバラツキ具合を検定しているのに対し(つまり、ペアの差の平均値がどうであるかを検定している)、対応のないt検定では両群の測定値のバラツキ具合を検定しているからです。
具体的な検定法法の違いについては、本選択肢の解説から離れるので止めておきましょう。
続いて「各群の標準偏差が大きいほど、有意な差があるという結果が生じやすい」という点の検証をしていきましょう。
まず「標準偏差」とは、データのバラツキ具合をバシッとひとつの数値で表したものになります。
具体的な計算方法としては、個々の値と平均値の差の2乗の平均の√をとった値ですから、「個々の値が平均値から離れている程度をひとつの数値で示したもの」ということもできますね。
対応のないt検定では、標本Aの平均値と標本Bの平均値を比べることになりますが、本選択肢にある「各群の標準偏差が大きい」とは、このAB両方のデータのバラつき具合が大きいということを指しています。
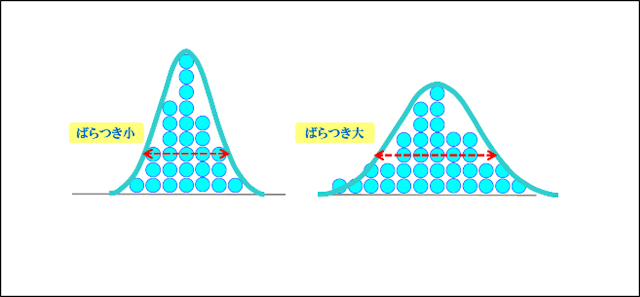
標準偏差はSDと表記され、±1SD内に正規分布の約68%が納まるように設定されています。
つまり、データのバラつき具合が大きいか小さいかで、描かれる正規分布の形が異なってきます。
上記のように、標準偏差が小さい(バラつきが小さい)と正規分布はとんがった高い山の形になります。
対して、標準偏差が大きい(バラつきが大きい)と正規分布は平べったい低い山の形になります。
すなわち、標準偏差が大きいということは、裾野が広がっているので、平均から値が離れているデータが多くある可能性が高いということになりますね。
一般的に、標準偏差が小さい(バラつきが小さい)と、有意な差があるという結果が生じやすいとされています。
これは考えてみれば当たり前で、t検定では平均値の差を比べるわけですが、標準偏差が大きいと「データが平均値から遠く離れている」ということになり、その平均値をあまり信用することができなくなります(要は外れ値が多いデータであるということ)。
これに対して、標準偏差が小さいと、たとえ平均値の差が小さかったとしても「意味の有る差」だとみなすことができ、有意差が出やすくなるということです。
言い換えれば、同じ平均値であったとしても、標準偏差が大きいことで、その平均値の差が「意味のある差」と見なされなくなるというわけですね。
他にも有意な差が生じやすい状況があり、それは「平均値の差が大きい場合」と「サンプルサイズ(データ量)が大きい場合」です。
平均値の差を比べるのがt検定ですから、「平均値の差が大きい場合」には有意な差が得られやすいのはわかるだろうと思います。
また、サンプルサイズが小さければ、偶然の要素が大きくなり、一見して差があるように思えても、意味の有る差とは言えないこともしばしばです。
これに対して、サンプルサイズが大きければ、偶然の要素が小さくなるので、意味の有る差だとみなしやすく、有意差が出るのです。
このように、t検定において有意差が出やすい状況は…
- 平均値の差が大きい
- 標準偏差が小さい
- サンプルサイズが大きい
…とされています。
自分が納得できるように、その理由も含めて理解するようにしておきましょう。
以上より、本選択肢の「対応のない2群のt検定では、各群の標準偏差が大きいほど」という状況では、有意な差が生じにくくなると言えます。
よって、選択肢④は誤りと判断できます。
⑤ K. Pearsonの相関係数の有意性検定では、サンプルサイズが小さいほど、帰無仮説の上側確率に基づく棄却の限界値は小さい。
こちらは選択肢③とほぼ同じような内容が問われています。
違いは「t検定」か「相関係数」であるか、ですね。
選択肢①で「t検定では、自由度が大きいほど、帰無仮説が棄却されるポイントが小さくなっていく(帰無仮説の上側確率に基づく棄却の限界値は小さくなる)」という、一種の「ルール」のようなものをお示ししたと思います。
これと同じような「ルール」が相関係数の有意性検定でもあるのです。
それは、選択肢③で「1000という標本があれば、相関係数(r)は「0.062」という極めて小さな相関係数であっても「有意な差がある」となってしまいます」と述べましたが、これのことを指しています。
つまり「相関において、標本数(サンプルサイズ)が大きいほど、相関が弱くても(相関係数の値が低くても)、有意差がありになってしまう」のです。
端的に言い換えると「サンプルサイズが大きいほど、有意差ありになりやすい(帰無仮説が棄却されやすい)」ということです。
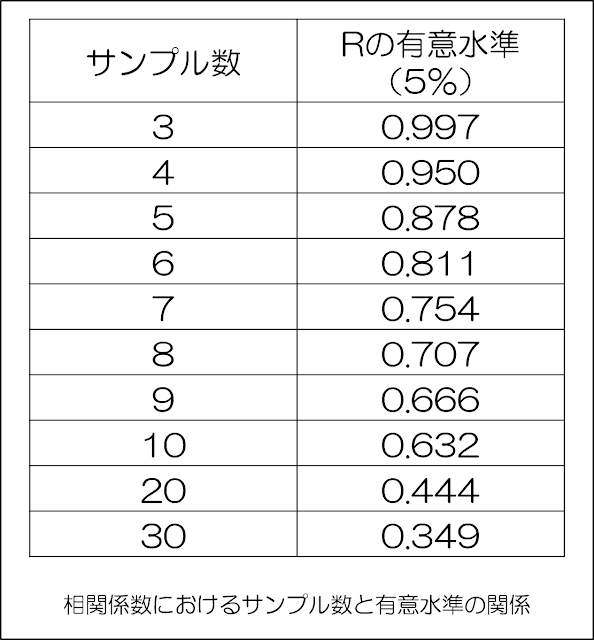
わかりやすく説明するため、まずはサンプルサイズと有意水準との関係について示していきましょう。
このように、サンプルサイズが増すほどに、有意水準は低い数字になっていることがわかりますね。
これに対して、本選択肢では「サンプルサイズが小さいほど、帰無仮説の上側確率に基づく棄却の限界値は小さい」について問うています。
当然、サンプルサイズが小さいと有意水準は高い数字になっていくことになります。
すなわち、上記で言えば、サンプルサイズが小さいと「上側パーセント点」つまり「棄却の限界値」は、右側に寄っていくこと(0から遠ざかっていく)になります。
これは「棄却の限界値」が大きくなることを意味していますね。
上の表でも、サンプルサイズが小さいほど、有意水準(これが棄却の限界値)が大きい数字になっていることがわかるはずです。
以上より、「K. Pearsonの相関係数の有意性検定では、サンプルサイズが小さいほど、帰無仮説の上側確率に基づく棄却の限界値は大きい」というのが正しい表現になると言えますから、選択肢⑤の内容は間違いですね。
よって、選択肢⑤は誤りと判断できます。